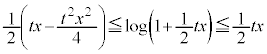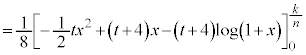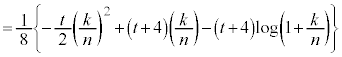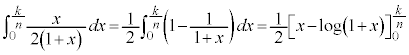慶大理工数学'21年[4]
(1) aは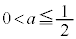 を満たす定数とする。
を満たす定数とする。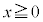 の範囲で不等式
の範囲で不等式
が成り立つことを示しなさい。
(2) bを実数の定数とする。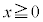 の範囲で不等式
の範囲で不等式 が成り立つようなbの最小値は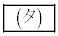 である。
である。
(3) nとkを自然数とし、
とおく。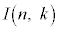 を求めると、
を求めると、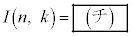 である。また
である。また である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (3)の積分計算が簡単にできないので、他の方法を考えることになります。(1)(2)の不等式は何のためなのか、と考えると、道が開けると思います。
(1) 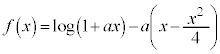 とおくと、微分して、
とおくと、微分して、 ∴ 
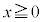 において、
において、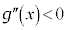 より、
より、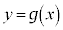 のグラフは上に凸で各点における接線から下側にあります。
のグラフは上に凸で各点における接線から下側にあります。
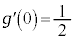 より、
より、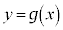 の
の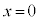 における接線は、
における接線は、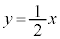
以上より、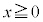 において、
において、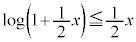
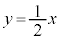 が
が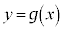 の
の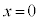 における接線、ということは、
における接線、ということは、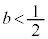 のとき、
のとき、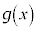 が
が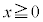 において単調増加で
において単調増加で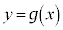 のグラフが上に凸なことと
のグラフが上に凸なことと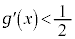 (
(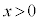 )であることから、原点を通る直線
)であることから、原点を通る直線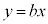 は、
は、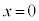 において
において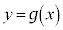 と交わることになります。この交点のx座標を
と交わることになります。この交点のx座標を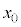 とすると、
とすると、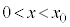 においては、
においては、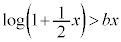 となってしまいます。よって、bの最小値は
となってしまいます。よって、bの最小値は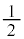 ......[タ]
......[タ]注.上記ではややいい加減に見えるかもしれません。厳格に考えるなら、まず、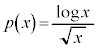 とすると、
とすると、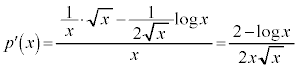 ,
, とすると
とすると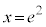 ,
,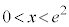 において
において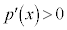 、
、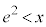 において
において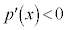 より
より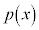 は
は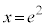 において最大値
において最大値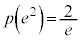 をとります。よって、
をとります。よって、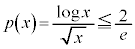 ,両辺に
,両辺に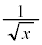 をかけて
をかけて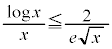 ,
,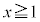 においては
においては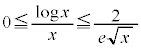 ,ここで
,ここで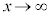 とすると、
とすると、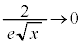 であって、はさみうちの原理より
であって、はさみうちの原理より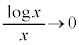 ,これより、
,これより、 つまり、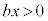 より
より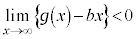 です。
です。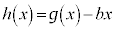 とおき、
とおき、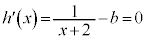 とすると
とすると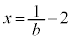 ,
,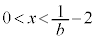 において
において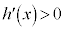 ,
,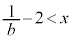 において
において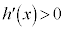 より、
より、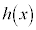 は
は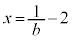 において最大値
において最大値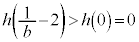 をとり、
をとり、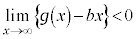 と合わせて、方程式
と合わせて、方程式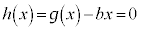 は、
は、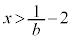 において解
において解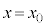 を持ちます。このとき、
を持ちます。このとき、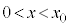 において
において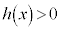 つまり、
つまり、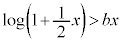 となります。
となります。
ですが、試験場でこんなことやっていたら合格は無理です。慶応理工では、結果のみが問われているのでムダな時間を使わないようにしてください。
(3) (1)(2)の不等式を利用して、はさみうち、に持ち込みます。
被積分関数の中では、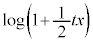 となっているので、(2)は、xに
となっているので、(2)は、xに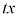 (
(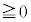 )を代入して使うことになります。(1)は、
)を代入して使うことになります。(1)は、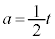 とすると、
とすると、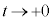 としても、
としても、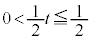 を満たせるのか不明です。従って
を満たせるのか不明です。従って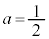 としなければならず、そうすると、ここでも、xに
としなければならず、そうすると、ここでも、xに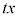 を代入して使います。
を代入して使います。
つまり、(1)において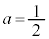 ,(2)において
,(2)において とし、(1)(2)においてxに
とし、(1)(2)においてxに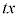 (
(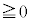 )を代入することにより、
)を代入することにより、 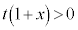 より、
より、ここで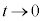 とすると、
とすると、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
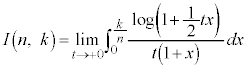
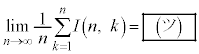



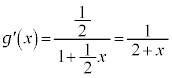 ,
,
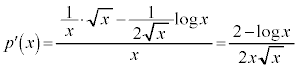 ,
,