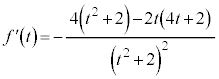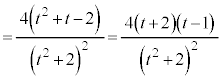�c�嗝�H���w'21�N[1]
t �������Ƃ��A���W���ʏ�̒���l�F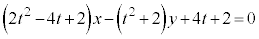 ���l����B
���l����B
(1) ����l��t �̒l�ɂ�炸�A��_��ʂ�B���̒�_�̍��W�� �ł���B
�ł���B
(2) ����l�̌X����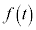 �Ƃ���B
�Ƃ���B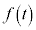 �̌X�����ŏ��ƂȂ�̂�
�̌X�����ŏ��ƂȂ�̂� �̂Ƃ��ł���A�ő�ƂȂ�̂�
�̂Ƃ��ł���A�ő�ƂȂ�̂� �̂Ƃ��ł���B�܂��Aa�������Ƃ���Ƃ��At �Ɋւ��������
�̂Ƃ��ł���B�܂��Aa�������Ƃ���Ƃ��At �Ɋւ��������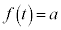 �����傤��1�̎����������悤��a�̒l�����ׂċ��߂�ƁA
�����傤��1�̎����������悤��a�̒l�����ׂċ��߂�ƁA �ł���B
�ł���B
(3) t �������S�̂��Ƃ��A����l���ʉ߂���̈��S�Ƃ���B�܂��Ak�������Ƃ���B������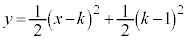 ���̈�S�Ƌ��L�_�����悤��k�̒l�͈̔͂�
���̈�S�Ƌ��L�_�����悤��k�̒l�͈̔͂�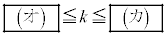 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�o��҂̗v���́A(1)(2)�̌��ʂ𗘗p����(3)�������A�Ƃ������Ƃ��낤�Ǝv���܂��B(3)���A�v������Ă���͉݂̂̂Ȃ̂ŁA�ׂ������_�I���t���͒Njy����ƃ��_�Ɏ��Ԃ��g�����ƂɂȂ�܂��B
(1) ����l�̎��F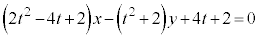 �@����@�@��t �ɂ��Đ�������ƁA
�@����@�@��t �ɂ��Đ�������ƁA 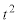 �̌W���At �̌W���A�萔����0�ɂ���ƁA
�̌W���At �̌W���A�萔����0�ɂ���ƁA������S�Ė������̂́A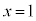 �C
�C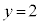
���̂Ƃ��At �������Ȃ�l���Ƃ��Ă��A�@���������܂��B����āA����l��t �̒l�ɂ�炸�ʂ��_�̍��W�́A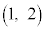 ......[�A]�@(��_��ʂ钼�����Q��)
......[�A]�@(��_��ʂ钼�����Q��)
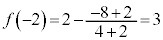 �C
�C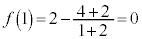
����āA�����\�́A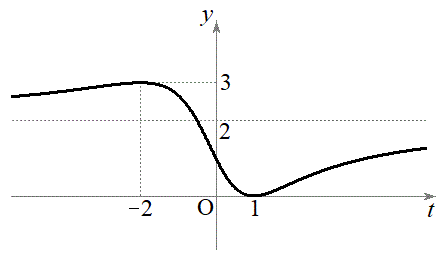
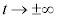 �̂Ƃ��A
�̂Ƃ��A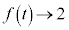 �@(���̋Ɍ����Q��)
�@(���̋Ɍ����Q��)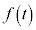 ���O���t�͉E�}�̂悤�ɂȂ�܂��B�����\���A
���O���t�͉E�}�̂悤�ɂȂ�܂��B�����\���A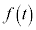 ���ŏ��ɂ���t �́A
���ŏ��ɂ���t �́A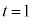 ......[�C]�C
......[�C]�C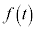 ���ő�ɂ���t �́A
���ő�ɂ���t �́A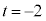 ......[�E]�C�O���t���A������
......[�E]�C�O���t���A������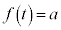 �����傤��1�̎�����������a�̒l�́A
�����傤��1�̎�����������a�̒l�́A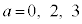 ......[�G]�@(�����@�̕������ւ̉��p(2)���Q��)
......[�G]�@(�����@�̕������ւ̉��p(2)���Q��)
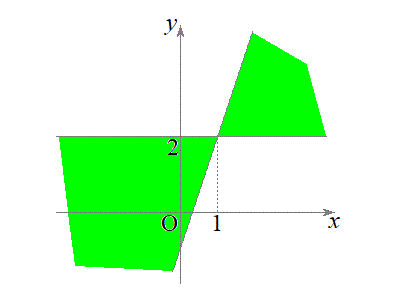 (3) ����l�́A�@��
(3) ����l�́A�@��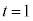 �Ƃ���ƁA
�Ƃ���ƁA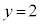 �C�@��
�C�@��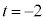 �Ƃ����
�Ƃ����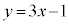 �ƂȂ�܂��B
�ƂȂ�܂��B����l�́At �������S�̂��Ƃ��A(1)���At �̒l�Ɋւ�炸�_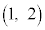 ��ʉ߂��A(2)���A�X����0����3�܂ŕω�����̂ŁA�E�}���ΐF���F���̂悤�ȗ̈�S��ʉ߂��܂��B
��ʉ߂��A(2)���A�X����0����3�܂ŕω�����̂ŁA�E�}���ΐF���F���̂悤�ȗ̈�S��ʉ߂��܂��B
������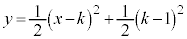 �́A����
�́A����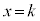 �C���_��
�C���_��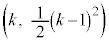 �ł��B
�ł��B
���������̈�S��ʉ߂��邽�߂ɂ́A������������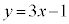 �C����
�C����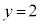 �̂����ꂩ�Ƌ��L�_�������Ƃ��K�v�\���ŁA����
�̂����ꂩ�Ƌ��L�_�������Ƃ��K�v�\���ŁA����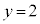 �Ƌ��L�_�������߂ɂ́A�������̒��_��y���W��2�ȉ��ł��邱�Ƃ��K�v�\���Ȃ̂ŁA���߂�����́A
�Ƌ��L�_�������߂ɂ́A�������̒��_��y���W��2�ȉ��ł��邱�Ƃ��K�v�\���Ȃ̂ŁA���߂�����́A
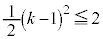 �@����A�@�܂��́A
�@����A�@�܂��́A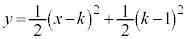 ��
��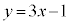 ��A�������Ƃ��Ɏ����������@����B
��A�������Ƃ��Ɏ����������@����B
�Ƃ������ƂɂȂ�܂��B
�A���A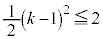 �C
�C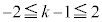 �@��
�@�� 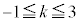 �@����C
�@����C
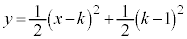 ��
��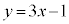 ��A�����āA
��A�����āA ����x��2���������͎����������̂ŁA���ʎ�D�ɂ��āA 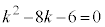 �Ƃ���ƁA
�Ƃ���ƁA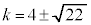 �Ȃ̂ŁA
�Ȃ̂ŁA �@����D
�@����D�����ŁA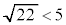 ���A
���A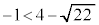 �ɒ��ӂ��A�C�܂��͇D�ł���A�������͗̈�S�Ƌ��L�_�����̂ŁA
�ɒ��ӂ��A�C�܂��͇D�ł���A�������͗̈�S�Ƌ��L�_�����̂ŁA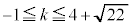
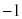 ......[�I]�C
......[�I]�C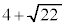 ......[�J]
......[�J]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B