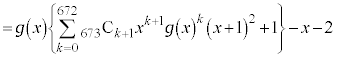�c�嗝�H���w'21�N[2]
(1) ���f��α��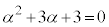 �����Ƃ���B���̂Ƃ��A
�����Ƃ���B���̂Ƃ��A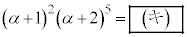 �ł���B�܂��A
�ł���B�܂��A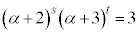 �ƂȂ鐮��s�Ct�̑g�����ׂċ��߁A���߂�ߒ��ƂƂ��ɉ�(1)�ɋL�q���Ȃ����B
�ƂȂ鐮��s�Ct�̑g�����ׂċ��߁A���߂�ߒ��ƂƂ��ɉ�(1)�ɋL�q���Ȃ����B
(2) ������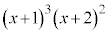 ��
��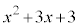 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏��� �C�]���
�C�]��� �ł���B�܂��A
�ł���B�܂��A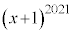 ��
��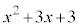 �Ŋ������Ƃ��̗]���
�Ŋ������Ƃ��̗]��� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�㔼���Ίp�̐������g��Ȃ��Ɖł��Ȃ��̂ŁA�ӂ���Ίp�֗̕��Ȑ������g�����Ȃ��Ă��Ȃ��Ƃ܂��������m��܂���B
(1) 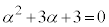 �@����@�@���A
�@����@�@���A 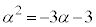 �@����A
�@����A�����p���āA
������A����ɇA��p���āA
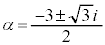 �@����B
�@����B�ȉ��A���������ŁA
�� 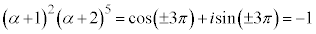 ......[�L]
......[�L]
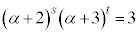 �@����E
�@����E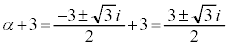
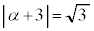 �C
�C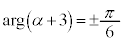 �@����F
�@����F����ƇD��p����ƁA�E�̐�Βl�ƕΊp�́A
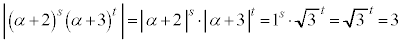 �@��
�@�� 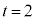 �@����G
�@����G
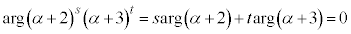 �@(�� 3�͐��̎���������A
�@(�� 3�͐��̎���������A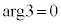 )
)�D�C�F�C�G���A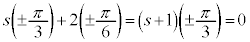 n�𐮐��Ƃ��āA�Ίp(��ʊp)�̐����F�u���镡�f��z�̕Ίp
n�𐮐��Ƃ��āA�Ίp(��ʊp)�̐����F�u���镡�f��z�̕Ίp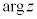 (��ʊp)�̈��
(��ʊp)�̈��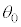 �Ƃ���
�Ƃ���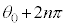 ������̊p�v�ɂ��A
������̊p�v�ɂ��A 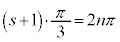 �@(
�@(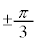 �̕�����n�̐����Ɋ܂߂�)�@��
�̕�����n�̐����Ɋ܂߂�)�@�� 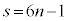
�ȏ���A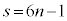 �C
�C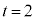 (n�͐���) ......[��]
(n�͐���) ......[��]
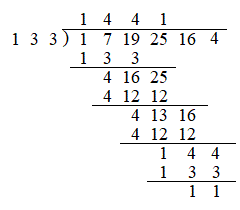 (2)
(2) 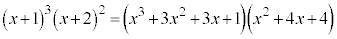
�����ۂ�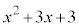 �Ŋ���(�������̏��Z���Q��)�ƁA�E�̂悤�ɂȂ�A����
�Ŋ���(�������̏��Z���Q��)�ƁA�E�̂悤�ɂȂ�A����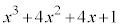 ......[�N]�C�]���
......[�N]�C�]���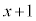 ......[�P]�ł��B
......[�P]�ł��B
�㔼�́A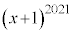 �����ۂɓW�J���ď��Z���s���킯�ɂ͂����Ȃ��̂ŁA�H�v���K�v�ł��B�藝�𗘗p���܂��B
�����ۂɓW�J���ď��Z���s���킯�ɂ͂����Ȃ��̂ŁA�H�v���K�v�ł��B�藝�𗘗p���܂��B
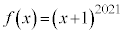 �C
�C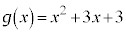 �Ƃ����ƁA
�Ƃ����ƁA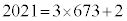 ���A
���A ����āA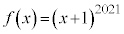 ��
��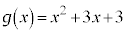 �Ŋ������Ƃ��̗]��́A
�Ŋ������Ƃ��̗]��́A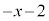 ......[�R]
......[�R]
[�ʉ�]�@�Ίp�𗘗p���邱�Ƃ��ł��܂��B
�C���A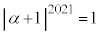
������A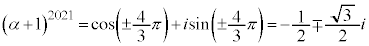 �@����H
�@����H
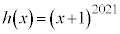 ��
��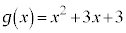 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���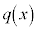 �C�]��(1����)��
�C�]��(1����)��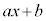 �Ƃ���ƁA
�Ƃ���ƁA �B��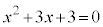 ��2���̕�����'�{'��
��2���̕�����'�{'��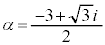 �C'�|'��
�C'�|'��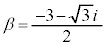 �Ƃ���(�����藝���Q��)�A
�Ƃ���(�����藝���Q��)�A �H�̕�����'�|'��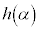 �C'�{'��
�C'�{'��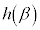 �ł��B
�ł��B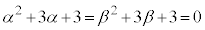 ���A
���A 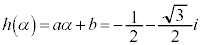 �@����I
�@����I
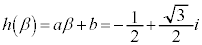 �@����J
�@����J�J�|�I���A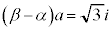
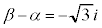 ���A
���A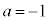
�I�ɑ������ƁA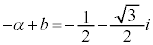
�� 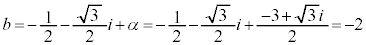 ����āA
����āA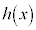 ��
��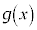 �Ŋ������]��́A
�Ŋ������]��́A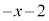 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
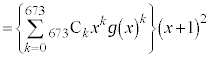
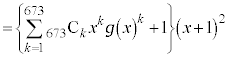
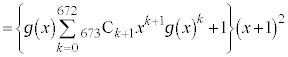
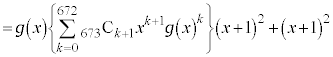
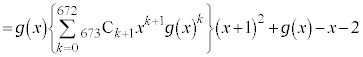 �@(
�@(