�c�嗝�H���w'21�N[5]
���W���ʏ�ŁA���_O��ʂ�A ������x�N�g���Ƃ��钼����l�Ƃ����B�������A
������x�N�g���Ƃ��钼����l�Ƃ����B�������A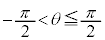 �Ƃ���B
�Ƃ���B
(1) 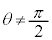 �Ƃ���B����l�̖@���x�N�g���ŁAy���������ł���A�傫����1�̃x�N�g����
�Ƃ���B����l�̖@���x�N�g���ŁAy���������ł���A�傫����1�̃x�N�g����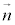 �Ƃ����B�_P
�Ƃ����B�_P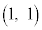 �ɑ��A
�ɑ��A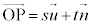 �ƕ\���B
�ƕ\���B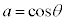 �C
�C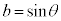 �Ƃ��āAs�Ct�̂��ꂼ���a�Cb�ɂ��Ă�1�����ŕ\����
�Ƃ��āAs�Ct�̂��ꂼ���a�Cb�ɂ��Ă�1�����ŕ\���� �C
�C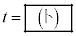 �ł���B
�ł���B
�_P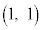 ���璼��l�ɐ��������낵�A����l�Ƃ̌�_��Q�Ƃ���B�������A�_P������l��ɂ���Ƃ��́A�_Q��P�Ƃ���B�ȉ��ł́A
���璼��l�ɐ��������낵�A����l�Ƃ̌�_��Q�Ƃ���B�������A�_P������l��ɂ���Ƃ��́A�_Q��P�Ƃ���B�ȉ��ł́A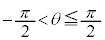 �Ƃ���B
�Ƃ���B
(2) ����PQ�̒����́A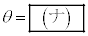 �̂Ƃ��ő�ƂȂ�B
�̂Ƃ��ő�ƂȂ�B
����ɁA�_R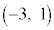 ���璼��l�ɐ��������낵�A����l�Ƃ̌�_��S�Ƃ���B�������A�_R������l��ɂ���Ƃ��́A�_S��R�Ƃ���B
���璼��l�ɐ��������낵�A����l�Ƃ̌�_��S�Ƃ���B�������A�_R������l��ɂ���Ƃ��́A�_S��R�Ƃ���B
(3) ����QS��1�F3�ɓ�������_��T�Ƃ����Bθ��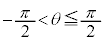 �����Ȃ��瓮���Ƃ��A�_T
�����Ȃ��瓮���Ƃ��A�_T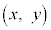 ���������O�Ղ̕�������
���������O�Ղ̕������� �ł���B
�ł���B
(4) 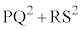 �̍ő�l��
�̍ő�l�� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@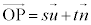 ���ꎟ�����̌`�ɏ����Ă���A�Ƃ������Ƃ����܂����p����ƁA�ȒP�ɉ������Ƃ��ł��܂��B�݂̖̂��Ȃ̂ŁA�������ɍ��������m�F�����炠�܂�ו��ɑ����Ȃ��悤�ɂ��܂��傤�B
���ꎟ�����̌`�ɏ����Ă���A�Ƃ������Ƃ����܂����p����ƁA�ȒP�ɉ������Ƃ��ł��܂��B�݂̖̂��Ȃ̂ŁA�������ɍ��������m�F�����炠�܂�ו��ɑ����Ȃ��悤�ɂ��܂��傤�B
(1) 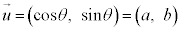 �C
�C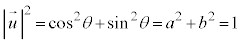 �@����@
�@����@ 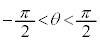 �ɂ����ẮA
�ɂ����ẮA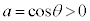 �ł��B
�ł��B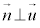 ,
, 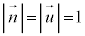 �Ȃ̂ŁA
�Ȃ̂ŁA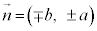 (��������)�ƂȂ�܂����A
(��������)�ƂȂ�܂����A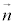 ��y�����͐��Ȃ̂ŁA
��y�����͐��Ȃ̂ŁA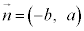 �ł�(�@���A
�ł�(�@���A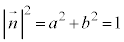 �ł�)�B
�ł�)�B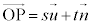 ���A
���A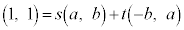 �@����A
�@����A�A���ӂ�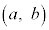 �Ƃ��������Ƃ�(t ���������܂�)�ƁA
�Ƃ��������Ƃ�(t ���������܂�)�ƁA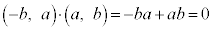 ���A
���A 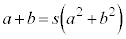 �C�@���A
�C�@���A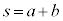 ......[�e]
......[�e]�A���ӂ�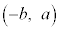 �Ƃ̓��ς��Ƃ�(s���������܂�)�ƁA
�Ƃ̓��ς��Ƃ�(s���������܂�)�ƁA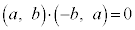 ���A
���A 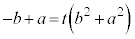 �C�@���A
�C�@���A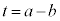 ......[�g]
......[�g]
(2) ����PQ�̒���d�́A�_P�ƒ���l�Ƃ̋����ł����A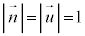 �Ȃ̂�(1)�ŋ��߂�t �̐�Βl�̂��Ƃł��B
�Ȃ̂�(1)�ŋ��߂�t �̐�Βl�̂��Ƃł��B 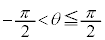 ���A
���A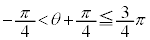 �C
�C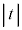 �́A
�́A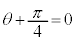 �C�܂�A
�C�܂�A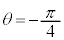 �̂Ƃ��ő�l
�̂Ƃ��ő�l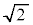 ���Ƃ�܂��B
���Ƃ�܂��B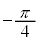 ......[�`]
......[�`]
(3) 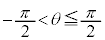 �Ȃ̂ŁA
�Ȃ̂ŁA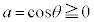 �C
�C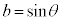 �́A
�́A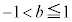 �ł��B
�ł��B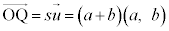 �C�܂��A
�C�܂��A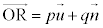 �Ƃ����ƁA
�Ƃ����ƁA 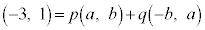 �@����B
�@����B�B���ӂ�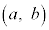 �Ƃ̓��ς��Ƃ�(q���������܂�)�ƁA�@���A
�Ƃ̓��ς��Ƃ�(q���������܂�)�ƁA�@���A 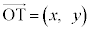 �Ƃ���ƁA
�Ƃ���ƁA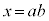 �C
�C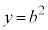
����ć@���A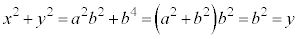 �C�]���āA�_T�̕`���O���̕������́A
�C�]���āA�_T�̕`���O���̕������́A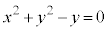 �ł��B
�ł��B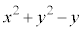 ......[�c]
......[�c]
(4) 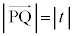 �C
�C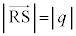 �ł��B�B���ӂ�
�ł��B�B���ӂ�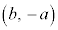 �Ƃ̓��ς��Ƃ�(p���������܂�)�ƁA
�Ƃ̓��ς��Ƃ�(p���������܂�)�ƁA 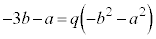 �C�@���A
�C�@���A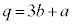
�����[�g]�̌��ʂ��A
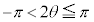 �Ȃ̂ŁA
�Ȃ̂ŁA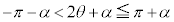
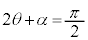 �C�܂�
�C�܂�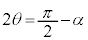 �̂Ƃ��A
�̂Ƃ��A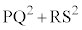 �́A�ő�l
�́A�ő�l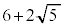 ......[�k]
......[�k]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B