���嗝�n���w'02�N�O��[5]
a�Cb�Cc�������Ƃ���B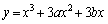 ��
��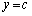 �̃O���t�����قȂ�3�̌�_�����Ƃ����B���̂Ƃ�
�̃O���t�����قȂ�3�̌�_�����Ƃ����B���̂Ƃ�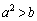 ���������邱�Ƃ������A����ɂ����̌�_��x���W�̂��ׂĂ͊J���
���������邱�Ƃ������A����ɂ����̌�_��x���W�̂��ׂĂ͊J���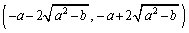 �Ɋ܂܂�Ă��邱�Ƃ������B
�Ɋ܂܂�Ă��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3���������̉��Ɋւ�����ł��B��蕶����x�̊J���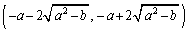 �Ƃ����̂́A
�Ƃ����̂́A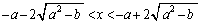 �Ƃ����͈�(���[���܂܂Ȃ�)�̂��Ƃł��B
�Ƃ����͈�(���[���܂܂Ȃ�)�̂��Ƃł��B
��A������ƁA
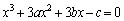 ����@
����@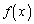 �Ƃ����܂��B
�Ƃ����܂��B
��Ӑ����̂��߂ɁA3���������@��3�̑��قȂ�������Ă悢�̂ł����A���̂��߂ɂ́A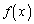 ���ɑ�l�Ƌɏ��l�������A�ɑ�l�����ŋɏ��l�����ƂȂ邱�Ƃ��K�v�\���ł��B
���ɑ�l�Ƌɏ��l�������A�ɑ�l�����ŋɏ��l�����ƂȂ邱�Ƃ��K�v�\���ł��B
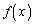 ���ɑ�l�Ƌɏ��l�������߂ɁA���Ȃ��Ƃ��A2��������
���ɑ�l�Ƌɏ��l�������߂ɁA���Ȃ��Ƃ��A2��������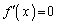 �����قȂ�2�����������K�v������܂��B�]���āA2��������
�����قȂ�2�����������K�v������܂��B�]���āA2��������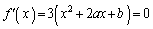 �̔��ʎ�D�͐��ł�(2���������̈�ʘ_���Q��)�B
�̔��ʎ�D�͐��ł�(2���������̈�ʘ_���Q��)�B
�� 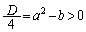
�� 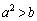 ����A
����A
�A�̏������ɁA2��������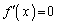 ��2����
��2����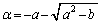 �C
�C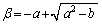 �Ƃ��܂��B
�Ƃ��܂��B
�ɑ�l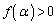 �C�ɏ��l
�C�ɏ��l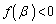 �ł���A
�ł���A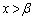 �ɂ����āA
�ɂ����āA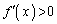 ���
���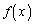 �͒P�������ł��B
�͒P�������ł��B
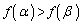 �C�܂��A
�C�܂��A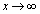 �̂Ƃ�
�̂Ƃ�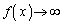 �Ȃ̂ŁA3��������
�Ȃ̂ŁA3��������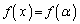 ��
��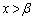 �͈̔͂ɉ�p�������܂��B�܂��A
�͈̔͂ɉ�p�������܂��B�܂��A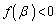 �C
�C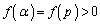 �Ȃ̂ŁA3��������
�Ȃ̂ŁA3��������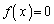 ��
��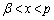 �͈̔͂�1�̉��������܂��B
�͈̔͂�1�̉��������܂��B
�܂��A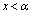 �ɂ����āA
�ɂ����āA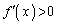 ���
���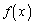 �͒P�������ł��B
�͒P�������ł��B
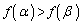 �C�܂��A
�C�܂��A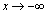 �̂Ƃ��A
�̂Ƃ��A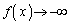 �Ȃ̂ŁA3��������
�Ȃ̂ŁA3��������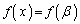 ��
��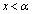 �͈̔͂ɉ�q�������܂��B�܂��A
�͈̔͂ɉ�q�������܂��B�܂��A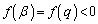 �Ȃ̂ŁA3��������
�Ȃ̂ŁA3��������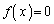 ��
��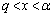 �͈̔͂�1�̉��������܂��B
�͈̔͂�1�̉��������܂��B
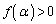 �C
�C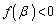 �ł����āA
�ł����āA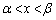 �ɂ�����
�ɂ�����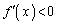 ���
���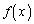 �͒P�������ŁA3��������
�͒P�������ŁA3��������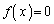 ��
��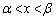 �͈̔͂�1�̉��������܂��B
�͈̔͂�1�̉��������܂��B
�ȏ���A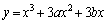 ��
��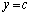 �̃O���t�����قȂ�3�̌�_�����Ƃ��A3�̌�_��x���W�A�܂�A3��������
�̃O���t�����قȂ�3�̌�_�����Ƃ��A3�̌�_��x���W�A�܂�A3��������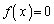 ��3�̉��̂��ׂẮA
��3�̉��̂��ׂẮA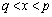 �͈̔͂ɂ���܂��B ����B
�͈̔͂ɂ���܂��B ����B
3��������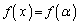 �C�܂�A
�C�܂�A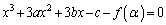 �͏d��α�Ɖ�p�����̂ŁA���ƌW���̊W���A
�͏d��α�Ɖ�p�����̂ŁA���ƌW���̊W���A
�� 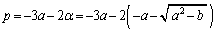
3��������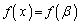 �C�܂�A
�C�܂�A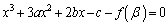 �͏d��β �Ɖ�q�����̂ŁA���ƌW���̊W���A
�͏d��β �Ɖ�q�����̂ŁA���ƌW���̊W���A
�� 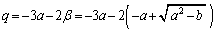
����āA�B���A3��������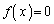 �́A
�́A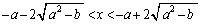 �͈̔͂ɈقȂ�3�������������܂��B
�͈̔͂ɈقȂ�3�������������܂��B
�܂�A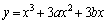 ��
��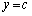 �̃O���t��3��_��x���W�̂��ׂĂ͊J���
�̃O���t��3��_��x���W�̂��ׂĂ͊J���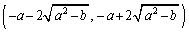 �Ɋ܂܂�Ă��܂��B
�Ɋ܂܂�Ă��܂��B
���̖��ɂ��ẮA�������낢�Z�I������܂��B��w�ւ̐��w'05�N6�����ɓ��e�����A�ٍe�����Q�Ƃ��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B