京大理系数学'03年前期[6]
nチームがリーグ戦を行う。すなわち、各チームは他のすべてのチームとそれぞれ1回ずつ対戦する。引き分けはないものとし、勝つ確率はすべて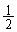
で、各回の勝敗は独立に決まるものとする。このとき、
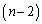勝1敗のチームがちょうど2チームである確率を求めよ。ただし、nは3以上とする。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 考えにくい確率の問題です。
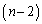勝1敗になる2チーム(Ａ，Bとします)をnチームの中から選ぶ方法は、
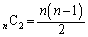通りあります(組み合わせを参照)。
この2チームの勝敗のパターンは、AがBに勝つ、BがAに勝つ、の2通りあります。
ここで、AがBに勝ったとして、Aは1敗するので、負けた相手をCとします。Cの選び方は、A，B以外の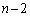
チームから1チームを選ぶので、
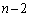通りあります。
Bは既にAに負けているので、1敗になるためには、Cに勝つことになります。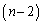
勝1敗のチームはちょうど2チームしかできないので、Cは、A，B，C以外の
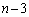チームのどれか少なくとも1チームには負けていることになります。これは、
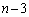チームの全てに勝つという事象の余事象です。この確率は、
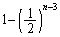です。
さて、Aが特定の1チームにだけ負けて、残りの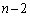
チームに勝つ確率は、
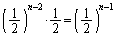(独立試行の確率を参照)
Aが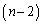
勝1敗のとき、Bは既にAに負けているので、Bも
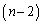勝1敗となるためには、BはA以外の
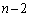チームに全勝します。この確率は、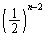
以上より、求める確率は、
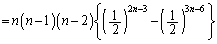......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 