���嗝�n���w'05�N�O��[5]
k�𐳂̐����Ƃ��A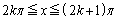 �͈̔͂Œ�`���ꂽ2�Ȑ�
�͈̔͂Œ�`���ꂽ2�Ȑ�
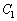 �F
�F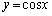 �C�@
�C�@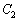 �F
�F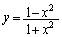
���l����B
(1) 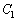 ��
��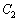 �͋��L�_�������Ƃ������A���̓_�ɂ�����
�͋��L�_�������Ƃ������A���̓_�ɂ�����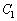 �̐ڐ��͓_
�̐ڐ��͓_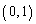 ��ʂ邱�Ƃ������B
��ʂ邱�Ƃ������B
(2) 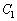 ��
��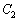 �̋��L�_�͂���1�ł��邱�Ƃ��ؖ�����B
�̋��L�_�͂���1�ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�͓��ł��B
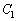 �F
�F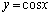 �@����@�C
�@����@�C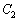 �F
�F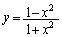 �@����A�@�Ƃ��܂��B
�@����A�@�Ƃ��܂��B
�A�̑S����x�ɑ��鑝���\�͈ȉ��̒ʂ�(���̑������Q��)�B�A�ɂ����āA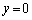 �Ƃ���ƁA
�Ƃ���ƁA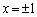
�S�����ōl�����Ƃ��̇A�̃O���t��x���Ƃ̌�_��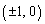
�]���āAk�𐳂̐����Ƃ��āA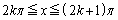 �ɂ����āA
�ɂ����āA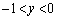
�@�ɂ��āA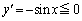 (
(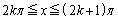 �Ck�F���̐���)�@(�����̌������Q��)
�Ck�F���̐���)�@(�����̌������Q��)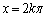 �̂Ƃ��A
�̂Ƃ��A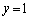 �C
�C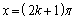 �̂Ƃ��A
�̂Ƃ��A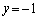
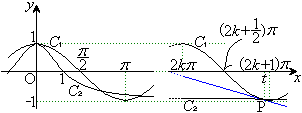 ����āA
����āA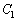 �͂��͈̔͂ɂ����ĒP�������ŁA2�_
�͂��͈̔͂ɂ����ĒP�������ŁA2�_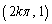 �C
�C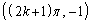 ��ʂ�܂��B
��ʂ�܂��B
�ȏ���A2�Ȑ��́A���͈̔͂ɂ����āA���L�_�������܂�(�E�}�Q��)�B
���̋��L�_P��x���W��t�Ƃ��܂��By���W�́A 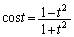 �@����B
�@����B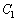 ��P�ɂ������ڐ��́A
��P�ɂ������ڐ��́A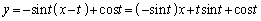 �@����C
�@����C�B���A
�Ƃ���ŁAt���A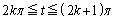 ��������A
��������A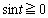 �ł����āA
�ł����āA ����ƇB���C�ɑ������ƁA
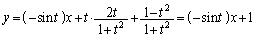 �@����D
�@����D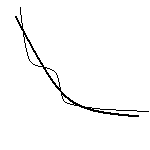
(2) (1)�����ł́A���L�_�����݂��邱�Ƃ͌����Ă��A���L�_���u����1�v�Ƃ������Ƃ͌����܂���B�E�}�̂悤�ɁA2�Ȑ��Ƃ��P�������ł����Ă��A�悶���悤�ɂȂ��Ă���ꍇ�ɂ́A�����̋��L�_�����݂���ꍇ�����邩��ł��B
�Ƃ����āA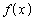 ���P�������ł��邱�Ƃ�������A
���P�������ł��邱�Ƃ�������A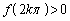 �C
�C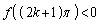 ����A���L�_������1�ƌ������Ƃ��ł��܂��B
����A���L�_������1�ƌ������Ƃ��ł��܂��B
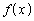 ���P�������ł��邱�Ƃ������ɂ́A
���P�������ł��邱�Ƃ������ɂ́A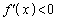 ��������悢�̂ł����A����͐��藧���܂���B���̕ӂ�������ƒ��ׂĂ����o���ƁA��ςȂ��ƂɂȂ�܂��B������ł́A���߂Ɍ�����K�v������܂��B
��������悢�̂ł����A����͐��藧���܂���B���̕ӂ�������ƒ��ׂĂ����o���ƁA��ςȂ��ƂɂȂ�܂��B������ł́A���߂Ɍ�����K�v������܂��B
��������l���Ă����̂łȂ��Ƃ���ƁA�@�ƇA��A���������������狤�L�_���l���Ă������ƂɂȂ�܂��B
�@�ƇA��A������ƁA ����́A�ƂĂ����������ȕ������ł͂���܂���B
�Ⴆ�A���͈̔͂�2��t�Cu�����Ƃ��āA
�Ƃ��Ă݂Ă��A�����_���o�Ă��܂���B
���̕ӂŎ�����ł͍s���l�܂��Ă��܂������m��܂���B
���������Ƃ��ɁA��l�������̂́A(1)�𗘗p����̂��낤�Ƃ������Ƃł��B
(1)�ł́A���L�_�ɂ�����ڐ����o�Ă��܂��B�n�n�[���A�ڐ��𗘗p����̂��낤�ȁA�Ƃ������ƂɂȂ�킯�ł��B
���̊F����́A������ōs���l�܂�����A�K���A��蕶��ǂݕԂ��āA�����Ƃ��Ă���|�C���g���Ȃ����A�`�F�b�N����悤�ɂ��܂��傤�B
�D���A���L�_P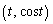 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A �Ə����܂��B���̐ڐ���(1)���A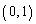 ��ʂ�܂��B(1)�̃O���t���A
��ʂ�܂��B(1)�̃O���t���A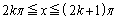 �ɂ����āA
�ɂ����āA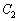 ��x����������ʂ�܂��B�Ƃ������Ƃ́A���L�_P��y���W�͕��ł��B
��x����������ʂ�܂��B�Ƃ������Ƃ́A���L�_P��y���W�͕��ł��B
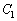 �́A
�́A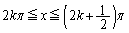 �ɂ����ẮA
�ɂ����ẮA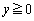 �̕�����ʂ�܂����A
�̕�����ʂ�܂����A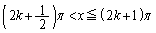 �ɂ����ẮA
�ɂ����ẮA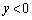 �̕�����ʂ�܂��B
�̕�����ʂ�܂��B
���L�_P��y���W�����Ƃ������Ƃ́A���L�_P��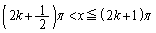 �͈̔͂ɑ��݂��Ă���Ƃ������Ƃł��BP�ƈقȂ鋤�L�_Q
�͈̔͂ɑ��݂��Ă���Ƃ������Ƃł��BP�ƈقȂ鋤�L�_Q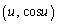 ������Ɖ��肷��(
������Ɖ��肷��(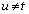 �C
�C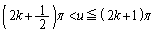 )�ƁA�D�Ɠ��l�ɂ��āAQ�ɂ�����ڐ��́A
)�ƁA�D�Ɠ��l�ɂ��āAQ�ɂ�����ڐ��́A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B