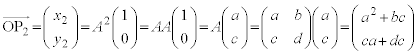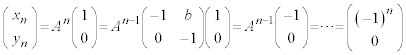���嗝�n���w'09�N��[4]
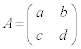 ��
��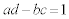 ���݂����s��Ƃ���(a�Cb�Cc�Cd�͎���)�B���R��n�ɑ��ĕ��ʏ�̓_
���݂����s��Ƃ���(a�Cb�Cc�Cd�͎���)�B���R��n�ɑ��ĕ��ʏ�̓_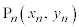 ��
��
�ɂ���߂�B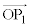 ��
��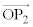 �̒�����1�̂Ƃ��A���ׂĂ�n�ɑ���
�̒�����1�̂Ƃ��A���ׂĂ�n�ɑ���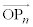 �̒�����1�ł��邱�Ƃ������B������O�͌��_�ł���B
�̒�����1�ł��邱�Ƃ������B������O�͌��_�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�x�N�g���̑傫����ς��Ȃ�1���ϊ�(����ϊ��ƌ����܂��B����ϊ��ɂ��ẮA1���ϊ�����2���Q��)�́A��]�ϊ�(�s��1)�Ƌ��f�ϊ�(�s��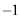 )�Ɍ�����A�Ƃ����A�c�嗝�H'09[B1]�Ɠ���e�[�}�̖��ł��B����̖{��ł́A
)�Ɍ�����A�Ƃ����A�c�嗝�H'09[B1]�Ɠ���e�[�}�̖��ł��B����̖{��ł́A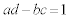 �Ƃ������������Ă���̂ʼn�]�ϊ��ɂȂ�܂��B�܂��A���̂ق��A�X�^�[�g��
�Ƃ������������Ă���̂ʼn�]�ϊ��ɂȂ�܂��B�܂��A���̂ق��A�X�^�[�g��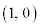 �Ȃ̂ŁAx�������ɒ�����ς��Ȃ�1���ϊ�(�ŗL�l
�Ȃ̂ŁAx�������ɒ�����ς��Ȃ�1���ϊ�(�ŗL�l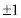 �ɑ���ŗL�x�N�g����
�ɑ���ŗL�x�N�g����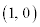 )���������݂����܂��B
)���������݂����܂��B
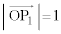 ���A
���A
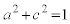 �@����@
�@����@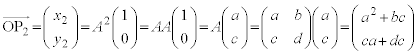
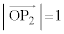 ���A
���A
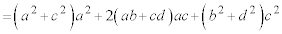
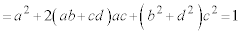 �@(�� �@)
�@(�� �@)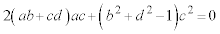 �@(��
�@(�� 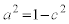 )
)
�� 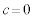 �܂���
�܂��� 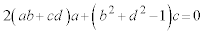
(i) 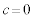 �̂Ƃ��A
�̂Ƃ��A �@���A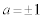
�܂��A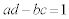 ���A
���A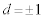 �@(��������)�܂�A
�@(��������)�܂�A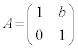 �C�܂��́A
�C�܂��́A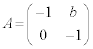 �@(b�͔C�ӂ̎���)�O�҂ł́A
�@(b�͔C�ӂ̎���)�O�҂ł́A ��҂ł́A
������ɂ��Ă��A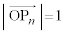 �ł��B
�ł��B
(ii) 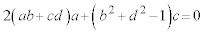 �̂Ƃ��A
�̂Ƃ��A �@���A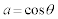 �C
�C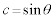 �Ƃ������Ƃ��ł��܂��B����āA
�Ƃ������Ƃ��ł��܂��B����āA 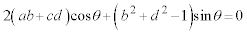 �@����A
�@����AA�CB�������Ƃ��āA
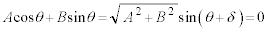 �@����B�@�������A
�@����B�@�������A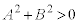 �ł���A
�ł���A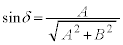 �C
�C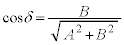
�B��θ �Ɋւ�炸�������邽�߂ɂ́A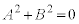 �C�܂�A
�C�܂�A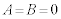
����āA�A���A 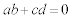 �@����C
�@����C
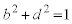 �@����D
�@����D�C���A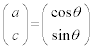 ��
��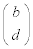 �͒�������(�������Q��)�̂ŁA
�͒�������(�������Q��)�̂ŁA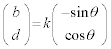 �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B
�D���A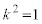 �C
�C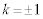
�� 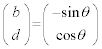 �C�܂��́A
�C�܂��́A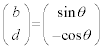
�O�҂ł́A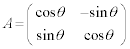
����́A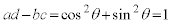 ���������݂����Ă��܂��B
���������݂����Ă��܂��B
�s��A�͌��_�̉��ɔ����v���Ɋpθ ��]����1���ϊ���\���s��Ȃ̂ŁA�x�N�g�� �̑傫����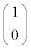 �̑傫���Ɠ�����1�ł��B����āA
�̑傫���Ɠ�����1�ł��B����āA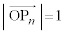 �ł��B
�ł��B
��҂ł́A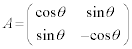
����́A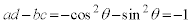 �ƂȂ�������݂����܂���(�ł����A���̂Ƃ���
�ƂȂ�������݂����܂���(�ł����A���̂Ƃ���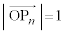 �ł�)�B
�ł�)�B
�ȏ���A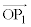 ��
��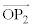 �̒�����1�̂Ƃ��A���ׂĂ�n�ɑ���
�̒�����1�̂Ƃ��A���ׂĂ�n�ɑ���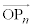 �̒�����1�ł��B
�̒�����1�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B