���嗝�n���w'13�N[3]
n�����R���Ƃ��A����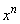 �𐮎�
�𐮎�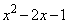 �Ŋ������]���
�Ŋ������]���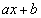 �Ƃ���B���̂Ƃ�a��b�͐����ł���A����ɂ������Ƃ��Ɋ����f���͑��݂��Ȃ����Ƃ������B
�Ƃ���B���̂Ƃ�a��b�͐����ł���A����ɂ������Ƃ��Ɋ����f���͑��݂��Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������ƌ����ڂɂ͓�₩�H�Ƃ������������Ȃ��ł��Ȃ��ł����A����Ă݂�ƈՖ�ł��B�ȑO�̏d���ȋ��吔�w�̖ʉe�͔��o������܂���B
����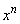 �𐮎�
�𐮎�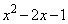 �Ŋ���ƁA2�����Ŋ���̂ŁA�]���1�����ł��B����
�Ŋ���ƁA2�����Ŋ���̂ŁA�]���1�����ł��B����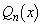 �C�]���
�C�]���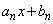 �Ƃ��܂�(�������̏��Z���Q��)�B
�Ƃ��܂�(�������̏��Z���Q��)�B
�����ł́A2��������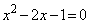 �̉�
�̉�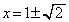 (
(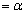 �Ƃ����܂�)�������Ă݂�̂���ł��B
�Ƃ����܂�)�������Ă݂�̂���ł��B
�������āA�{��́A2���������𗘗p�������������̖��ɋA�����܂��B
�ȉ��A���w�I�A�[�@�ɂ��ؖ����܂��B
(�T) 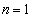 �̂Ƃ��A
�̂Ƃ��A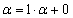 ���A
���A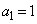 �C
�C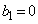 �ł��B
�ł��B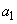 �C
�C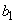 �Ƃ��ɐ����ŁA1��0���Ƃ��Ɋ����f���͑��݂��Ȃ��̂ŁA��ӂ͐������܂��B
�Ƃ��ɐ����ŁA1��0���Ƃ��Ɋ����f���͑��݂��Ȃ��̂ŁA��ӂ͐������܂��B (�U) 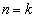 �̂Ƃ��A
�̂Ƃ��A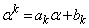 �Ƃ����āA
�Ƃ����āA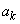 �C
�C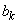 ���Ƃ��ɐ����ł���A���A
���Ƃ��ɐ����ł���A���A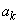 �C
�C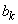 ���Ƃ��Ɋ����f���͑��݂��Ȃ��Ɖ���(����́A���w�I�A�[�@�̉���ł�)���܂��B
���Ƃ��Ɋ����f���͑��݂��Ȃ��Ɖ���(����́A���w�I�A�[�@�̉���ł�)���܂��B 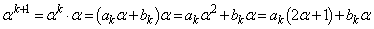 �@(��
�@(�� 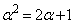 )
)�]���āA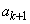 �C
�C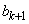 ���A
���A 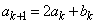 �C
�C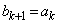 �@����@
�@����@�ƂȂ�悤�Ɍ��߂�A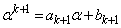 �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B
�܂��A�@���A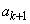 �C
�C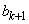 �͐����ł��B�����ŁA
�͐����ł��B�����ŁA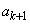 �C
�C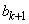 ���Ƃ��Ɋ����悤�ȑf��p�����݂���Ɖ���(����́A�w���@�̉���ł�)����ƁA
���Ƃ��Ɋ����悤�ȑf��p�����݂���Ɖ���(����́A�w���@�̉���ł�)����ƁA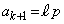 �C
�C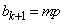 (
(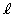 �Cm�͐���)�Ƃ������Ƃ��ł��܂��B�@���A
�Cm�͐���)�Ƃ������Ƃ��ł��܂��B�@���A 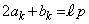 �C
�C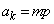
�� 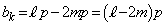
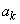 ��
��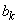 ���Ƃ��ɑf��p�Ŋ����邱�ƂɂȂ�A���w�I�A�[�@�̉���ɔ����܂��B����āA�u
���Ƃ��ɑf��p�Ŋ����邱�ƂɂȂ�A���w�I�A�[�@�̉���ɔ����܂��B����āA�u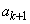 �C
�C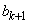 ���Ƃ��Ɋ����悤�ȑf��p�����݂���v�Ƃ�������͌��ŁA
���Ƃ��Ɋ����悤�ȑf��p�����݂���v�Ƃ�������͌��ŁA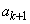 �C
�C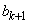 ���Ƃ��Ɋ����悤�ȑf��p�͑��݂��܂���B
���Ƃ��Ɋ����悤�ȑf��p�͑��݂��܂���B (�T)(�U)���An�����R���Ƃ��āA����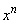 �𐮎�
�𐮎�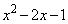 �Ŋ������]���
�Ŋ������]���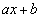 �Ƃ���ƁAa��b�͐����ł���A����ɂ������Ƃ��Ɋ����f���͑��݂��܂���B
�Ƃ���ƁAa��b�͐����ł���A����ɂ������Ƃ��Ɋ����f���͑��݂��܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B