���嗝�n���w'22�N�O��[6]
����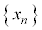 �C
�C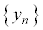 �����̎�
�����̎�
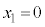 �C
�C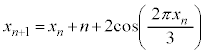 �@(
�@(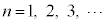 )�C
)�C
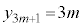 �C
�C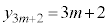 �C
�C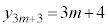 �@(
�@(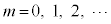 )
)
�ɂ���߂�B���̂Ƃ��A����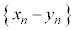 �̈�ʍ������߂�B
�̈�ʍ������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f����n�ɐ��l������Ă����Ό����Ă��܂����A���Ăɂ܂Ƃ߂�̂͂Ȃ��Ȃ���ςł��B
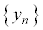 �ɂ��ẮA
�ɂ��ẮA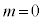 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A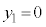 �C
�C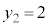 �C
�C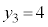
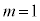 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A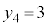 �C
�C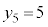 �C
�C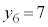
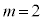 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A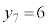 �C
�C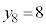 �C
�C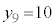
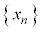 �ɂ��ẮA
�ɂ��ẮA
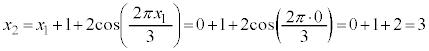
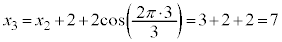
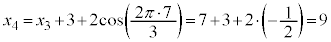
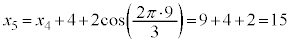
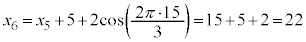
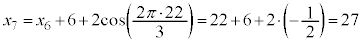
����ŁA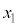 �C
�C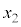 �C
�C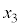 �C
�C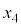 �C
�C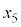 �C
�C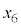 �C
�C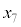 �C����Ɛi�߂Ă����ƁA3�̔{���A3�̔{���A3�̔{���{1�C3�̔{���A3�̔{���A3�̔{���{1�C3�̔{���C����ƁA3�����J��Ԃ���Ă��邱�Ƃ��킩��܂��B
�C����Ɛi�߂Ă����ƁA3�̔{���A3�̔{���A3�̔{���{1�C3�̔{���A3�̔{���A3�̔{���{1�C3�̔{���C����ƁA3�����J��Ԃ���Ă��邱�Ƃ��킩��܂��B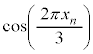 �̌`���炵�Ă��A
�̌`���炵�Ă��A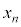 ��3�̔{��(�������Q��)���ǂ������|�C���g�ł��邱�Ƃ��킩��܂��B
��3�̔{��(�������Q��)���ǂ������|�C���g�ł��邱�Ƃ��킩��܂��B
�܂��A���̎���(��)�F
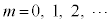 �Ƃ��āA
�Ƃ��āA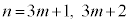 �̂Ƃ�
�̂Ƃ�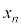 ��3�̔{���A
��3�̔{���A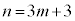 �̂Ƃ�
�̂Ƃ�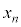 ��3�Ŋ����1�]�鐔
��3�Ŋ����1�]�鐔
(�T) 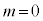 �̂Ƃ��A
�̂Ƃ��A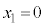 �C
�C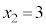 ��3�̔{���A
��3�̔{���A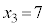 ��3�Ŋ����1�]�鐔�Ȃ̂ŁA(��)�͐������܂��B
��3�Ŋ����1�]�鐔�Ȃ̂ŁA(��)�͐������܂��B (�U) 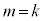 �̂Ƃ��A(��)����������Ɖ��肷��ƁA
�̂Ƃ��A(��)����������Ɖ��肷��ƁA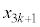 �C
�C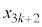 ��3�̔{���A
��3�̔{���A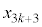 ��3�Ŋ����1�]�鐔�ł��B
��3�Ŋ����1�]�鐔�ł��B �^�Q�������A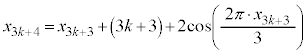 �@����@
�@����@
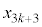 ��3�Ŋ����1�]�鐔�Ȃ̂ŁAp�𐮐��Ƃ��āA
��3�Ŋ����1�]�鐔�Ȃ̂ŁAp�𐮐��Ƃ��āA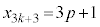 �Ƃ����ƁA
�Ƃ����ƁA ����āA�@���A
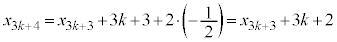 �@����A
�@����A����āA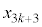 ��3�Ŋ����1�]�鐔�Ȃ̂�
��3�Ŋ����1�]�鐔�Ȃ̂�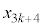 ��3�̔{���ł��B
��3�̔{���ł��B
�^�Q�������A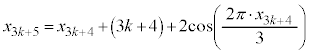
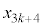 ��3�̔{���Ȃ̂ŁA
��3�̔{���Ȃ̂ŁA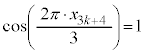 ���A
���A 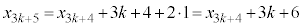 �@����B
�@����B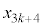 ��3�̔{���Ȃ̂�
��3�̔{���Ȃ̂�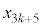 ��3�̔{���ł��B
��3�̔{���ł��B
�^�Q�������A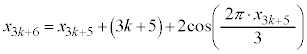
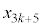 ��3�̔{���Ȃ̂ŁA
��3�̔{���Ȃ̂ŁA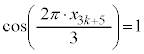 ���A
���A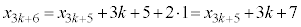 �@����C
�@����C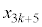 ��3�̔{���Ȃ̂�
��3�̔{���Ȃ̂�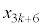 ��3�Ŋ����1�]�鐔�ł��B
��3�Ŋ����1�]�鐔�ł��B
����āA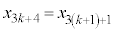 �C
�C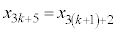 ��3�̔{���A
��3�̔{���A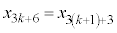 ��3�Ŋ����1�]�鐔�ŁA
��3�Ŋ����1�]�鐔�ŁA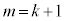 �̂Ƃ��ɂ�(��)�͐������܂��B
�̂Ƃ��ɂ�(��)�͐������܂��B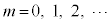 �ɂ��āA(��)���������܂��B
�ɂ��āA(��)���������܂��B
�܂��A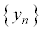 �Ɋւ���^�����A
�Ɋւ���^�����A
�B�ɂ�����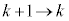 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A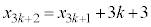 �@����G
�@����G
�C�ɂ�����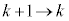 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A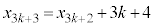 �@����H
�@����H
�A���A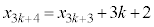 �@����I
�@����I
�D�C�G���A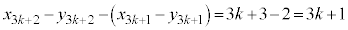 �@����J
�@����J
�E�C�H���A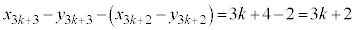 �@����K
�@����K
�F�C�I���A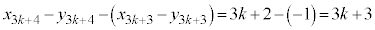 �@����L
�@����L
�J��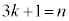 �C�K��
�C�K��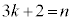 �C�L��
�C�L��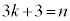 �Ƃ��邱�Ƃɂ��A�J�C�K�C�L���܂Ƃ߁An�����ׂĂ̎��R���Ƃ��āA
�Ƃ��邱�Ƃɂ��A�J�C�K�C�L���܂Ƃ߁An�����ׂĂ̎��R���Ƃ��āA
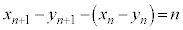 �@����M
�@����M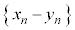 �ɂ��ẮA
�ɂ��ẮA
�ƂȂ��Ă���킯�ł����A�M�ɂ��A�K�������̌�����p���āA
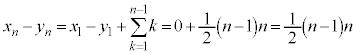 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@
�@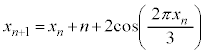 �@(
�@(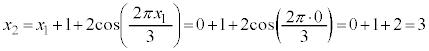
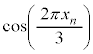 �̌`���炵�Ă��A
�̌`���炵�Ă��A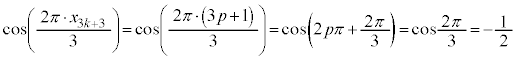
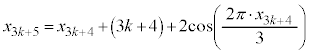
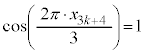 ���A
���A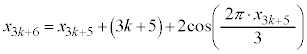
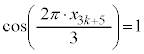 ���A
���A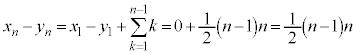 ......[��]
......[��]