京大理系数学'23年前期[1]
次の各問に答えよ。
問1 定積分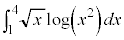 の値を求めよ。
の値を求めよ。 問2 整式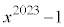 を整式
を整式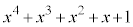 で割ったときの余りを求めよ。
で割ったときの余りを求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問1は、部分積分する計算問題です。問2は、余りを3次式として、1の5乗根を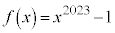 に代入し、因数定理を利用して4元連立方程式を解いてもできそうですが、計算が複雑になりそうなので、少し工夫します。
に代入し、因数定理を利用して4元連立方程式を解いてもできそうですが、計算が複雑になりそうなので、少し工夫します。
問1 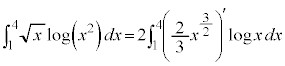 (部分積分法を参照)
(部分積分法を参照)
問2 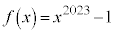 ,
,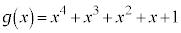 とおきます。
とおきます。 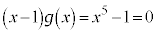 より、
より、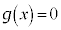 の解は、1の5乗根のうち1以外のものです。このうちの1つをαとすると、
の解は、1の5乗根のうち1以外のものです。このうちの1つをαとすると、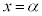 とすると、
とすると、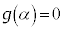 より、
より、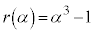 となりますが、αは4通りの値をとるので、
となりますが、αは4通りの値をとるので、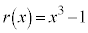 とならないか、と期待できます。実際に、
とならないか、と期待できます。実際に、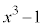 を
を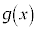 で割った余りは
で割った余りは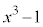 です。
です。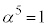 ,
,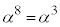 なので、
なので、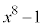 を
を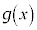 で割ってみると(多項式の除算を参照)、
で割ってみると(多項式の除算を参照)、となり余りは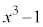 です。整式の除算をしなくても、
です。整式の除算をしなくても、 と変形すれば、すぐにわかります。
そこで、命題「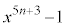 を
を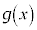 で割った余りは
で割った余りは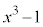 」を数学的帰納法で証明します。
」を数学的帰納法で証明します。 (I) 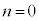 のとき、
のとき、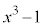 を
を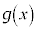 で割った余りは
で割った余りは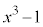 なので命題は成立します。
なので命題は成立します。 (II) 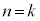 のとき、命題が成立し、
のとき、命題が成立し、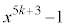 を
を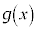 で割って、商が
で割って、商が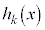 として、
として、 が成立すると仮定します。
両辺に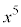 をかけると、
をかけると、 よって、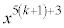 を
を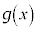 で割った余りは
で割った余りは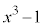 となるので、
となるので、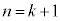 のときも命題は成立します。
のときも命題は成立します。 (I),(II),数学的帰納法により、命題は成立し、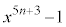 を
を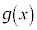 で割った余りは
で割った余りは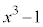 であり、
であり、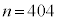 として、
として、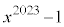 を
を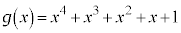 で割った余りは、
で割った余りは、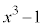 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 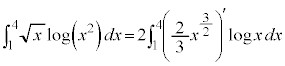 (部分積分法を参照)
(部分積分法を参照)