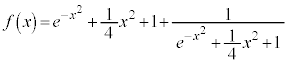京都大学理系2023年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の各問に答えよ。
問1 定積分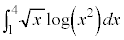
の値を求めよ。 問2 整式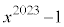
を整式
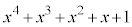で割ったときの余りを求めよ。 [解答へ]
[2] 空間内の4点O，A，B，Cは同一平面上にないとする。点D，P，Qを次のように定める。点Dは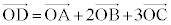
を満たし、点Pは線分OAを1：2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR：RDを求めよ。
[解答へ]
[3] nを自然数とする。1個のさいころをn回投げ、出た目を順に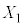
，
，･･････，
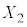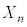とし、n個の数の積
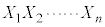をYとする。
(1) Yが5で割り切れる確率を求めよ。
(2) Yが15で割り切れる確率を求めよ。
[解答へ]
[4] 次の関数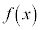
の最大値と最小値を求めよ。
ただし、eは自然対数の底であり、その値は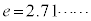
である。
[解答へ]
[5] Oを原点とするxyz空間において、点Pと点Qは次の3つの条件(a)，(b)，(c)を満たしている。
(a) 点Pはx軸上にある。
(b) 点Qはyz平面上にある。
(c) 線分OPと線分OQの長さの和は1である。
点Pと点Qが条件(a)，(b)，(c)を満たしながらくまなく動くとき、線分PQが通過してできる立体の体積を求めよ。
[解答へ]
[6] pを3以上の素数とする。また、θを実数とする。
(2) 
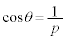のとき、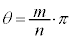
となるような正の整数m，nが存在するか否かを理由を付けて判定せよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
と
を
の式として表せ。