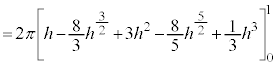���嗝�n���w'23�N�O��[5]
O�����_�Ƃ���xyz��Ԃɂ����āA�_P�Ɠ_Q�͎���3�̏���(a)�C(b)�C(c)�����Ă���B
(a) �_P��x����ɂ���B
(b) �_Q��yz���ʏ�ɂ���B
(c) ����OP�Ɛ���OQ�̒����̘a��1�ł���B
�_P�Ɠ_Q������(a)�C(b)�C(c)�����Ȃ��炭�܂Ȃ������Ƃ��A����PQ���ʉ߂��Ăł��闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����I�ɉ�]�̂̑̐όv�Z�̖��ł��B
����(a)���Ax����̓_P��x���W��p�Ƃ���ƁAP�̍��W��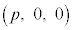 �ł��B����(c)��茴�_O����̋�����1�ȉ��ŁA
�ł��B����(c)��茴�_O����̋�����1�ȉ��ŁA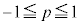 �ł��B�܂��A����(b)���yz���ʏ�ɓ_Q���Ƃ�܂��B
�ł��B�܂��A����(b)���yz���ʏ�ɓ_Q���Ƃ�܂��B
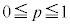 �̂Ƃ��A
�̂Ƃ��A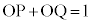 ���A
���A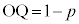 �ł����Ax����̓_
�ł����Ax����̓_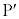
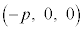 ���Ƃ�ƁA��͂�
���Ƃ�ƁA��͂�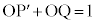 �ł���A�܂�
�ł���A�܂�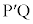 ��PQ��yz���ʂɊւ��đΏ̂ł��B�]���āA
��PQ��yz���ʂɊւ��đΏ̂ł��B�]���āA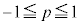 �Ƃ��Đ���PQ���ʉ߂��Ăł��闧�̂�S�Ƃ��āAS��yz���ʂɊւ��đΏ̂ł��B����āAS�̑̐ς́A
�Ƃ��Đ���PQ���ʉ߂��Ăł��闧�̂�S�Ƃ��āAS��yz���ʂɊւ��đΏ̂ł��B����āAS�̑̐ς́A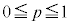 �Ƃ��čl�������̂̑̐ς�2�{�ł���A�Ȍ�
�Ƃ��čl�������̂̑̐ς�2�{�ł���A�Ȍ�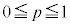 �Ƃ���S��
�Ƃ���S��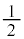 �̑̐ς��l���܂��B
�̑̐ς��l���܂��B
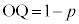 ���Ayz���ʏ�ɂ����ē_Q�́A���_�𒆐S�Ƃ��锼�a
���Ayz���ʏ�ɂ����ē_Q�́A���_�𒆐S�Ƃ��锼�a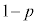 �̉~����̓_�ŁA
�̉~����̓_�ŁA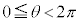 �Ƃ��āAQ�̍��W��
�Ƃ��āAQ�̍��W��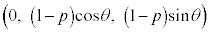 �ł��B
�ł��B
����PQ��̓_R�́A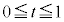 �Ƃ���(�����������Q��)�A
�Ƃ���(�����������Q��)�A
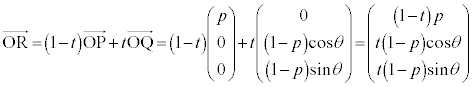 �@����@
�@����@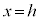 (
(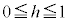 )�Ő����f�ʂ��l���܂��B
)�Ő����f�ʂ��l���܂��B
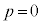 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A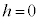 �̂Ƃ��ɂ̂ݒf�ʂ����݂��A�@��
�̂Ƃ��ɂ̂ݒf�ʂ����݂��A�@��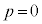 �Ƃ���ƁA
�Ƃ���ƁA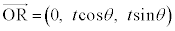 �ƂȂ�Ayz���ʏ�ɂ����āAR�́A���_O�𒆐S�Ƃ��锼�at �̉~����̓_(�~�̔}��ϐ��\�����Q��)�ł���A
�ƂȂ�Ayz���ʏ�ɂ����āAR�́A���_O�𒆐S�Ƃ��锼�at �̉~����̓_(�~�̔}��ϐ��\�����Q��)�ł���A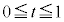 �Ȃ̂ŁAR�́A���_O�𒆐S�Ƃ��锼�a1�̉~����y�щ~�����̓_�ł��B�@����A
�Ȃ̂ŁAR�́A���_O�𒆐S�Ƃ��锼�a1�̉~����y�щ~�����̓_�ł��B�@����A
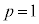 �̂Ƃ��AR��
�̂Ƃ��AR��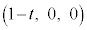 (
(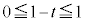 )��x�����x���W��0��1�̊Ԃł���1�_�ƂȂ�A����
)��x�����x���W��0��1�̊Ԃł���1�_�ƂȂ�A����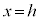 �Ő����f�ʂ�x�����1�_
�Ő����f�ʂ�x�����1�_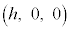 �ł��B
�ł��B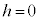 �̂Ƃ����_O�ɂȂ�܂������̂Ƃ��͇A�Ɋ܂܂�܂��B�@����B
�̂Ƃ����_O�ɂȂ�܂������̂Ƃ��͇A�Ɋ܂܂�܂��B�@����B
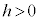 �Ƃ��āAR��x���W��h�Ƃ���ƁA
�Ƃ��āAR��x���W��h�Ƃ���ƁA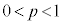 �̂Ƃ��ɂ́A�@���A
�̂Ƃ��ɂ́A�@���A
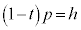 �@��
�@�� 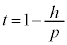
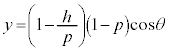 �C
�C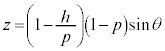
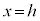 �Ő����f�ʏ�̓_R���A���̒f�ʏ�ŁA�_
�Ő����f�ʏ�̓_R���A���̒f�ʏ�ŁA�_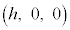 �𒆐S�Ƃ����a
�𒆐S�Ƃ����a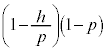 �̉~����̓_�ł��邱�Ƃ��Ӗ����܂��B���a��
�̉~����̓_�ł��邱�Ƃ��Ӗ����܂��B���a��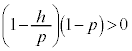 �ł��邽�߂ɁA
�ł��邽�߂ɁA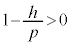 �C�܂�A
�C�܂�A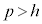 �ł��B
�ł��B
t ����h���Œ肵��p��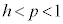 �͈̔͂��Ƃ��A���a
�͈̔͂��Ƃ��A���a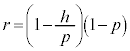 ���ǂ̂悤�Ȓl���Ƃ肤�邩�ׂ܂��B
���ǂ̂悤�Ȓl���Ƃ肤�邩�ׂ܂��B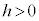 �ł����
�ł����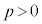 �ł����āA
�ł����āA
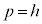 �̂Ƃ�
�̂Ƃ�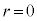 �C
�C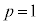 �̂Ƃ�
�̂Ƃ�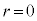 �C
�C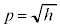 �̂Ƃ�
�̂Ƃ�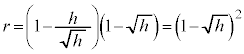 ���A�����\�͈ȉ��B
���A�����\�͈ȉ��B
| p | h | �@ | 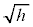 | �@ | 1 |
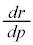 | �{ | �{ | 0 | �| | �| |
| r | 0 |  | 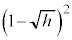 |  | 0 |
�����\���Ap��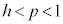 �͈̔͂��Ƃ��A���ar�́A
�͈̔͂��Ƃ��A���ar�́A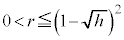 �͈̔͂̑S�Ă̒l���Ƃ蓾�܂��B
�͈̔͂̑S�Ă̒l���Ƃ蓾�܂��B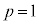 �̂Ƃ��̇B���܂߁A����
�̂Ƃ��̇B���܂߁A����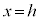 �Ő����f�ʂɂ����āA�_R�́A�_
�Ő����f�ʂɂ����āA�_R�́A�_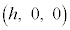 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a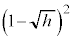 �̉~���̎���y�ѓ��������܂Ȃ������܂��B
�̉~���̎���y�ѓ��������܂Ȃ������܂��B
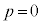 �̂Ƃ��̇A���A
�̂Ƃ��̇A���A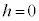 �̂Ƃ��ɂ́A���_
�̂Ƃ��ɂ́A���_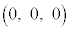 �𒆐S�Ƃ��锼�a1�̉~���̎���y�ѓ��������܂Ȃ������܂��B
�𒆐S�Ƃ��锼�a1�̉~���̎���y�ѓ��������܂Ȃ������܂��B
����āA����S��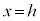 (
(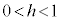 )�Ő����Ƃ��̒f�ʂ̖ʐς́A���a
)�Ő����Ƃ��̒f�ʂ̖ʐς́A���a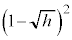 �̉~�̖ʐςƂȂ�A
�̉~�̖ʐςƂȂ�A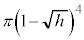 �ƂȂ�܂��B�@����C
�ƂȂ�܂��B�@����C
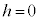 �̏ꍇ�́A���a1�̉~�̖ʐςŇC�Ɋ܂܂�܂��B
�̏ꍇ�́A���a1�̉~�̖ʐςŇC�Ɋ܂܂�܂��B
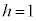 �̏ꍇ�́Ax�����1�_
�̏ꍇ�́Ax�����1�_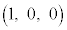 �ƂȂ�A�ʐς�0�ŇC�Ɋ܂܂�܂��B
�ƂȂ�A�ʐς�0�ŇC�Ɋ܂܂�܂��B
���D��L�ł͖ʓ|�Ȃ̂ŁA���ۂ̓��Ăł́A1�_�a0�C�ʐ�0�̉~�ƌĂԁA�Ƃ������Ƃɂ��āA�Ȍ��ȓ��Ăɂ܂Ƃ߂�ׂ��ł��B
�ȏ���AS�̑̐�V�́A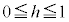 �͈̔͂Őϕ��������̂�2�{���āA
�͈̔͂Őϕ��������̂�2�{���āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 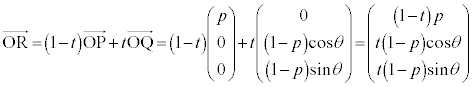 �@����@
�@����@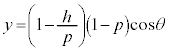 �C
�C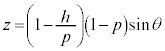
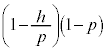 �̉~����̓_�ł��邱�Ƃ��Ӗ����܂��B���a��
�̉~����̓_�ł��邱�Ƃ��Ӗ����܂��B���a��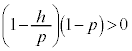 �ł��邽�߂ɁA
�ł��邽�߂ɁA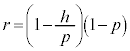 ���ǂ̂悤�Ȓl���Ƃ肤�邩�ׂ܂��B
���ǂ̂悤�Ȓl���Ƃ肤�邩�ׂ܂��B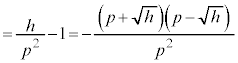
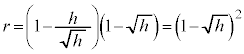 ���A�����\�͈ȉ��B
���A�����\�͈ȉ��B