���嗝�n���w'23�N�O��[6]
p��3�ȏ�̑f���Ƃ���B�܂��Aθ�������Ƃ���B
(2) 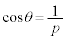 �̂Ƃ��A
�̂Ƃ��A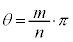 �ƂȂ�悤�Ȑ��̐���m�Cn�����݂��邩�ۂ��𗝗R��t���Ĕ��肹��B
�ƂȂ�悤�Ȑ��̐���m�Cn�����݂��邩�ۂ��𗝗R��t���Ĕ��肹��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@n�����R���Ƃ��āA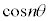 ��
��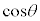 �̐���
�̐���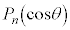 �Ƃ��ĕ\���A
�Ƃ��ĕ\���A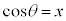 �Ƃ������̂�n���̃`�F�r�V�F�t�̑������ƌ����܂��B
�Ƃ������̂�n���̃`�F�r�V�F�t�̑������ƌ����܂��B
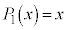 �C
�C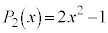 �C
�C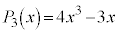 �C
�C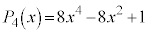 �ƂȂ��Ă��܂��B
�ƂȂ��Ă��܂��B
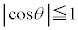 �C
�C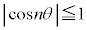 �Ȃ̂ŁA
�Ȃ̂ŁA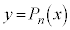 �̃O���t��
�̃O���t��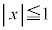 �̕����́A
�̕����́A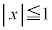 �C
�C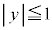 �̐����`�̒��ɂ҂�������܂�܂��B
�̐����`�̒��ɂ҂�������܂�܂��B
�ȉ��̉ŁA�Q�����@��p����̂̓`�F�r�V�F�t�̑������̖��ł͏퓅��i�Ȃ̂ŁA�q���g�������Ƃ������ł����A�L�����Ă����K�v������܂��B
(1) 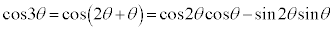
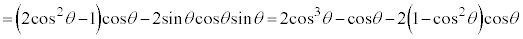
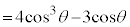 ......[��]
......[��]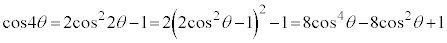 ......[��]
......[��]
(2) 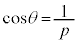 �̂Ƃ��A
�̂Ƃ��A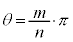 �ƂȂ�悤�Ȑ��̐���m�Cn�����݂���Ƃ��܂��B
�ƂȂ�悤�Ȑ��̐���m�Cn�����݂���Ƃ��܂��B (1)���炷��ƁA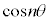 ��
��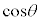 �ŕ\���Ƃǂ��Ȃ邩�A�Ƃ������Ƃ��|�C���g�ɂȂ肻���ł��B���̍ۂɁA
�ŕ\���Ƃǂ��Ȃ邩�A�Ƃ������Ƃ��|�C���g�ɂȂ肻���ł��B���̍ۂɁA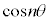 ��
��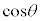 �̐����ŕ\���邱�Ƃ��A�[�I�Ɏ������ƂɂȂ�܂��B���̂��߂ɁA�a��ςɒ���������p���āA�Q��������邱�Ƃɂ��܂��B
�̐����ŕ\���邱�Ƃ��A�[�I�Ɏ������ƂɂȂ�܂��B���̂��߂ɁA�a��ςɒ���������p���āA�Q��������邱�Ƃɂ��܂��B 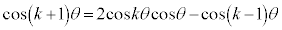 �@����@
�@����@������A�Ⴆ�A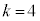 �Ƃ��āA
�Ƃ��āA �����ŁA�Ⴆ�A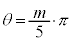 �C
�C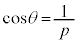 �Ƃ���ƁA
�Ƃ���ƁA 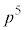 ��������ƁA
��������ƁA�E�ӂ́A3�ȏ�̑f��p��2��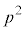 �̔{���ł����A16��p�̔{���ł͂Ȃ��̂ŁA����Ŗ��������������ł�(�������Q��)�B
�̔{���ł����A16��p�̔{���ł͂Ȃ��̂ŁA����Ŗ��������������ł�(�������Q��)�B
���āA�������Ė��������߂ɂ́A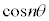 ��
��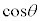 ��n���̐����W���̐����ł��邱�ƂƁA���̐����̍ō����̍��̌W�����f��p�̔{���ł͂Ȃ����Ƃ������Ă����K�v������܂��B
��n���̐����W���̐����ł��邱�ƂƁA���̐����̍ō����̍��̌W�����f��p�̔{���ł͂Ȃ����Ƃ������Ă����K�v������܂��B
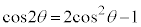 ��
��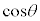 ��2���̐����W���̐����ŕ\����A�ō����̍��̌W����2�C(1)���A
��2���̐����W���̐����ŕ\����A�ō����̍��̌W����2�C(1)���A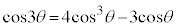 �C
�C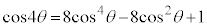 �͂��ꂼ��
�͂��ꂼ��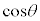 ��3���C4���̐����W���̐����ŕ\����A���̍ō����̍��̌W����
��3���C4���̐����W���̐����ŕ\����A���̍ō����̍��̌W����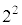 �C
�C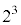 �ƂȂ邱�Ƃ���A
�ƂȂ邱�Ƃ���A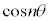 ��
��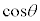 ��n���̐����W���̐����ŕ\����A�ō����̍��̌W����
��n���̐����W���̐����ŕ\����A�ō����̍��̌W����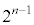 �ł��邱�Ƃ��\�������̂ŁA��������w�I�A�[�@�ŏؖ����܂��B
�ł��邱�Ƃ��\�������̂ŁA��������w�I�A�[�@�ŏؖ����܂��B (�T) 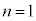 �̂Ƃ��A
�̂Ƃ��A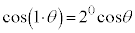 �ƂȂ�̂ŁA�\���͐������܂��B
�ƂȂ�̂ŁA�\���͐������܂��B (�U) 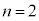 �̂Ƃ��A
�̂Ƃ��A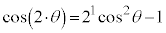 �ƂȂ�̂ŁA�\���͐������܂��B
�ƂȂ�̂ŁA�\���͐������܂��B (�V) 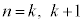 �̂Ƃ��A�\������������Ɖ��肷��ƁA
�̂Ƃ��A�\������������Ɖ��肷��ƁA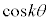 ��
��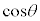 ��k���̐����W���̐����ŕ\���A�ō����̌W����
��k���̐����W���̐����ŕ\���A�ō����̌W����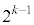 �C�܂��A
�C�܂��A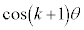 ��
��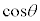 ��
��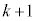 ���̐����W���̐����ŕ\���A�ō����̌W����
���̐����W���̐����ŕ\���A�ō����̌W����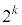 �ł��B
�ł��B �Ə����܂����A�@���A
����́A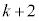 ����
����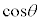 �̐����ł���A�W��
�̐����ł���A�W��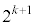 �C
�C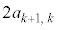 �C
�C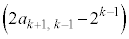 �C
�C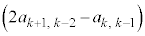 �C����C
�C����C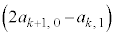 �C
�C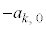 �͑S�Đ����ł����āA�ō����̍��̌W����
�͑S�Đ����ł����āA�ō����̍��̌W����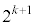 �ł��B����āA
�ł��B����āA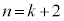 �̂Ƃ����\���͐������܂��B
�̂Ƃ����\���͐������܂��B (�T)�C(�U)�C(�V)�C���w�I�A�[�@���A���R��n�ɑ��āA�\���͐������A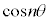 ��
��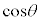 ��n���̐����W���̐����ŕ\����A�ō����̍��̌W����
��n���̐����W���̐����ŕ\����A�ō����̍��̌W����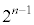 �ł��Bp��3�ȏ�̑f���Ƃ��āA
�ł��Bp��3�ȏ�̑f���Ƃ��āA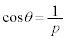 �̂Ƃ��A
�̂Ƃ��A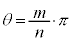 �ƂȂ�悤�Ȑ��̐���m�Cn�����݂���Ɖ��肷��ƁA
�ƂȂ�悤�Ȑ��̐���m�Cn�����݂���Ɖ��肷��ƁA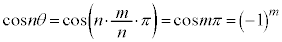 ���A
���A 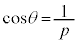 ���A
���A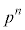 ��������ƁA
��������ƁA�E�Ӓ����ʓ��͐����ŁA�E�ӂ�3�ȏ�̑f��p�̔{���ł����A���ӂ�p�̔{���ł͂Ȃ�(�������Q��)�A���̓����͐��������Ȃ��̂ŁA���̐���m�Cn�����݂���A�Ƃ�������͌��ł��B�����A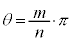 �ƂȂ�悤�Ȑ��̐���m�Cn�͑��݂��܂���B
�ƂȂ�悤�Ȑ��̐���m�Cn�͑��݂��܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B