���嗝�n���w'24�N�O��[4]
�^����ꂽ���R��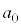 �ɑ��āA���R������Ȃ鐔��
�ɑ��āA���R������Ȃ鐔��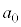 �C
�C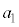 �C
�C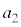 �C��������̂悤�ɒ�߂�B
�C��������̂悤�ɒ�߂�B
���̖₢�ɓ�����B
(1) 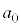 �C
�C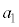 �C
�C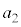 �C
�C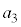 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��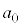 �����߂�B
�����߂�B
(2) 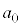 �C
�C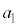 �C����C
�C����C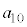 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��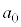 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͌�����܂Œ��ׂĂ��������ԓ��Ɏ��܂�܂��B(2)�͂��������킯�ɂ����Ȃ��̂ŁA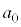 ���炷�ׂĊ���Ƃ����Q�������l���܂��B
���炷�ׂĊ���Ƃ����Q�������l���܂��B
(1) 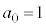 ���珇��
���珇��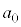 �Ɋ�����Ă݂܂��B�܂��A
�Ɋ�����Ă݂܂��B�܂��A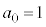 �Ƃ��Ă݂܂��B
�Ƃ��Ă݂܂��B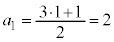 �C
�C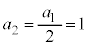 �C
�C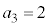 �C
�C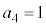 �ł��B
�ł��B 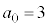 �Ƃ���ƁA
�Ƃ���ƁA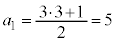 �C
�C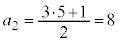 �C
�C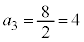 �C
�C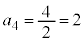 �ł��B
�ł��B
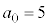 �Ƃ���ƁA
�Ƃ���ƁA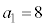 �ł��B
�ł��B
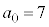 �Ƃ���ƁA
�Ƃ���ƁA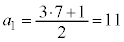 �C
�C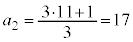 �C
�C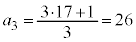 �ł��B
�ł��B
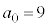 �Ƃ���ƁA
�Ƃ���ƁA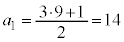 �ł��B
�ł��B
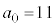 �Ƃ���ƁA
�Ƃ���ƁA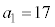 �C
�C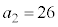 �ł��B
�ł��B
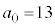 �Ƃ���ƁA
�Ƃ���ƁA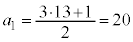 �ł��B
�ł��B
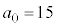 �Ƃ���ƁA
�Ƃ���ƁA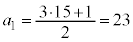 �C
�C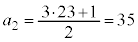 �C
�C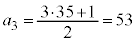 �ł��B����āA
�ł��B����āA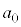 �C
�C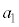 �C
�C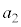 �C
�C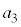 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��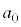 �́A
�́A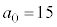 ......[��]
......[��]
(2) (1)�����Ă���ƁA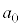 �̂݊�ł���ŏ��̎��R��
�̂݊�ł���ŏ��̎��R��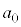 ��
��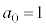 �C
�C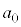 �C
�C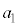 �����ׂĊ�ł���ŏ��̎��R��
�����ׂĊ�ł���ŏ��̎��R��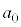 ��
��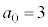 �C
�C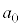 �C
�C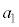 �C
�C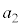 �����ׂĊ�ł���ŏ��̎��R��
�����ׂĊ�ł���ŏ��̎��R��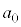 ��
��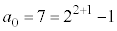 �C
�C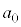 �C
�C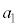 �C
�C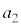 �C
�C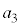 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��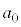 �́A
�́A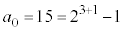 �ƂȂ��Ă���̂ŁA
�ƂȂ��Ă���̂ŁA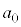 �C
�C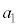 �C����C
�C����C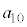 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��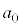 �́A
�́A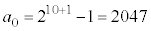 �ɂȂ肻���ł����A�܂����A�����܂őS�����ׂ�킯�ɂ͂����܂���B
�ɂȂ肻���ł����A�܂����A�����܂őS�����ׂ�킯�ɂ͂����܂���B �����ŁA�Q��������邱�Ƃ��l���܂��B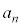 �C
�C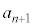 ���Ƃ��Ɋ���Ƃ��āA
���Ƃ��Ɋ���Ƃ��āA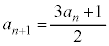 �@����@�@(2���ԑQ�������Q��)
�@����@�@(2���ԑQ�������Q��)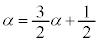 �@����A�@��
�@����A�@�� 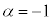
�@�|�A���A
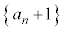 �́A����
�́A����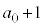 �C����
�C����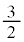 �����䐔���ł��B����āA
�����䐔���ł��B����āA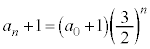 �@����B
�@����B�����ŁA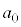 �`
�`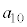 �����ׂĊ�ł��邽�߂ɂ́A
�����ׂĊ�ł��邽�߂ɂ́A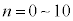 �̑S�Ăɂ��ćB�������ł���悢�킯�ł����A
�̑S�Ăɂ��ćB�������ł���悢�킯�ł����A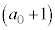 ��
��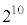 �Ŋ����ċ����C�܂�A
�Ŋ����ċ����C�܂�A �ł���A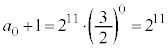 �C
�C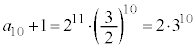 �C�������C
�C�������C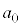 �̂��ׂĂ������ŁA
�̂��ׂĂ������ŁA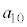 �`
�`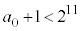 �̂��ׂĂ���ɂȂ�܂��B�܂��A
�̂��ׂĂ���ɂȂ�܂��B�܂��A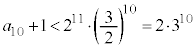 �̂��ׂĂŖ�蕶�̑Q�����͇@�ɂȂ�܂��B
�̂��ׂĂŖ�蕶�̑Q�����͇@�ɂȂ�܂��B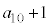 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A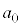 �́A
�́A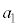 �����̐���
�����̐���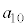 �Ŋ���̂ŁA�f������������Ƃ���2�̎w����1�����ŁA
�Ŋ���̂ŁA�f������������Ƃ���2�̎w����1�����ŁA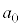 �������ɂȂ�܂���B�܂�A
�������ɂȂ�܂���B�܂�A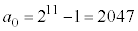 ����ɂȂ�܂���B����āA
����ɂȂ�܂���B����āA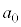 �C
�C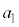 �C����C
�C����C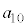 �����ׂĊ�ł���悤�ȍŏ��̎��R��
�����ׂĊ�ł���悤�ȍŏ��̎��R��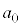 �́A
�́A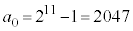 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B