���嗝�n���w'99�N���[6]
(1)  ��
��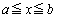 �ŘA���Ȋ��Ƃ���B���̂Ƃ��A
�ŘA���Ȋ��Ƃ���B���̂Ƃ��A 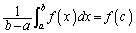 �@
�@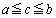
�ƂȂ�c�����݂��邱�Ƃ������B
(2) 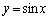 ��
��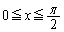 �̕�����
�̕����� �����y�����͂ސ}�`���Ay���̂܂��ɉ�]���ē����闧�̂��l����B���̗��̂�y���ɐ�����
�����y�����͂ސ}�`���Ay���̂܂��ɉ�]���ē����闧�̂��l����B���̗��̂�y���ɐ����� �̕��ʂɂ���Ċe�����̑̐ς��������Ȃ�悤��n�ɕ�������Ƃ��A
�̕��ʂɂ���Ċe�����̑̐ς��������Ȃ�悤��n�ɕ�������Ƃ��A �ɍł��߂����ʂ�y���W��
�ɍł��߂����ʂ�y���W��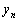 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A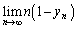 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͐ϕ��̕��ϒl�̒藝�ł��B(2)�́A��ؓ�ł͂����܂���B�Ɋ�d�ɂ��H�v���K�v�ł��B
(1)  (
(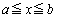 )�Ƃ����܂��B
)�Ƃ����܂��B  ��
��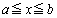 �ɂ����ĘA���ł����āA
�ɂ����ĘA���ł����āA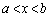 �ɂ����Ĕ����\�ŁA
�ɂ����Ĕ����\�ŁA �C
�C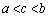
�ƂȂ�c�����݂��܂��B
����āA
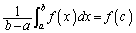 �C
�C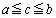
�ƂȂ�c�����݂��܂��B
(2) 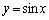 ��
�� �̕�����
�̕�����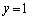 �����y�����͂ސ}�`���Ay���̂܂��ɉ�]���ē����闧�̂̑̐�V�́A
�����y�����͂ސ}�`���Ay���̂܂��ɉ�]���ē����闧�̂̑̐�V�́A  �ł�x��y�ŕ\�����Ƃ��ł��Ȃ��̂ŁA
�ł�x��y�ŕ\�����Ƃ��ł��Ȃ��̂ŁA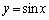 �ɂ���u���ϕ����s���܂��B
�ɂ���u���ϕ����s���܂��B
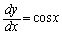 ���A
���A �Cy�F
�Cy�F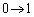 �̂Ƃ�x�F
�̂Ƃ�x�F
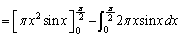
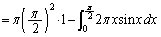 �@(�~�������̍l������p���Ē��ڂ��̎����������Ƃ��ł��܂��By���̂܂��̉�]�����Q��)
�@(�~�������̍l������p���Ē��ڂ��̎����������Ƃ��ł��܂��By���̂܂��̉�]�����Q��)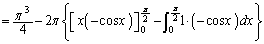
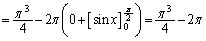 �@����@
�@����@��ӂ��A
 �@����A
�@����A�����ŁA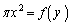 �Ƃ���(1)��p���A
�Ƃ���(1)��p���A  �C
�C �@����B
�@����B�Ƃ������̂ł����A �̋�̓I�Ȍ`�������Ȃ��̂ō���܂��B�ł����A
�̋�̓I�Ȍ`�������Ȃ��̂ō���܂��B�ł����A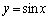 �Ȃ̂ŁA
�Ȃ̂ŁA �Ə������Ƃ͂ł��܂��B
�ƂȂ�܂��B
�������ćB���A
 �C
�C
�Ə����������Ƃ��ł��܂��B�A��p���āA
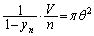 �@����C
�@����C���̂܂܂ł́A �̂Ƃ���θ ���ǂ��Ȃ邩�킩��Ȃ��̂ŁA
�̂Ƃ���θ ���ǂ��Ȃ邩�킩��Ȃ��̂ŁA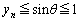 ��p���Ă͂��݂����̌`�����܂��B�C��θ �ɂ��ĉ����A
��p���Ă͂��݂����̌`�����܂��B�C��θ �ɂ��ĉ����A �� 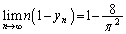 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B