���H�吔�w'05�N�O��[3]
D�a1�̉~�ՁAC��xy���ʂ̌��_�𒆐S�Ƃ��锼�a1�̉~���Ƃ���BD�����̏���(a)�C(b)�����ɖ������Ȃ���xyz��ԓ����Ƃ��AD���ʉ߂��镔���̑̐ς����߂�B
(a) D�̒��S��C��ɂ���B
(b) D������Ă��镽�ʂ͏�Ƀx�N�g��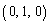 �ƒ�������B
�ƒ�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�`���݂ɂ������̂̑̐������߂���ł́A�����ɗ��̂̌`���Nj������A���鎲�ɐ����ȕ��ʂŗ��̂���Ă��̒f�ʐς��l���A�f�ʐς����ɉ����Đϕ����܂��B
���̖��ł́Az���ɐ����ɗ���K���̂��f�p�Ŏ�����₷���ł��傤�B
�~�̒��S��P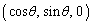 �ɂ���Ƃ��A����(b)���A�~�͕���
�ɂ���Ƃ��A����(b)���A�~�͕���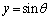 ����@ ��ɂ����āA�����zx���ʏ�܂�y���ƕ��s�ɕ��s�ړ�������ƁA�~�F
����@ ��ɂ����āA�����zx���ʏ�܂�y���ƕ��s�ɕ��s�ړ�������ƁA�~�F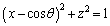 ����A �ɂȂ�܂��B
����A �ɂȂ�܂��B
�Ƃ���ŁAD�̒ʉ߂��镔���ɂł��闧��K��xy���ʁAyz���ʁAzx���ʂɊւ��đΏ̂Ȃ̂ŁA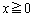 �C
�C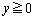 �C
�C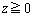 �̕�����K�̑̐ς��l���āA8�{���邱�Ƃɂ��܂��B
�̕�����K�̑̐ς��l���āA8�{���邱�Ƃɂ��܂��B
��Lθ ��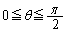 �͈̔͂ōl���A����K��z���ɐ����ȕ���
�͈̔͂ōl���A����K��z���ɐ����ȕ���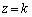 (
(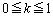 )�Ő����Ƃ��̐�����l���܂��B
)�Ő����Ƃ��̐�����l���܂��B
�܂��AP�ɒ��S������~��D��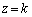 �Ő��Ă݂܂��B
�Ő��Ă݂܂��B
�A��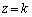 �Ƃ��āA
�Ƃ��āA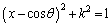
�� 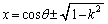 ����B
����B
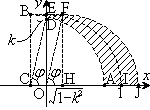 ������A����́A���[��
������A����́A���[��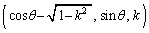 �C
�C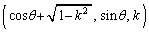 �Ƃ�������ł��B���̐����̒�����
�Ƃ�������ł��B���̐����̒�����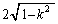 (k�ɂ݈̂ˑ����Aθ �ɂ͈ˑ����Ȃ�)�ŁA���̒��_�́A�~C��
(k�ɂ݈̂ˑ����Aθ �ɂ͈ˑ����Ȃ�)�ŁA���̒��_�́A�~C�� ��ɂ܂ŕ��s�ړ��������~����ɂ���܂��B���ǁA�~��D��
��ɂ܂ŕ��s�ړ��������~����ɂ���܂��B���ǁA�~��D�� �Ő��������xy���ʏ�܂ŕ��s�ړ�������ƁA�E�}�ΐ����̂悤�ɂȂ�܂��B
�Ő��������xy���ʏ�܂ŕ��s�ړ�������ƁA�E�}�ΐ����̂悤�ɂȂ�܂��B
�E�}�̉~��EI�́A�~C��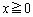 �C
�C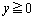 �̕����ł��B
�̕����ł��B
�B��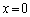 �Ƃ���ƁA
�Ƃ���ƁA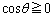 (�� ��1�ی��ōl���Ă���)���A
(�� ��1�ی��ōl���Ă���)���A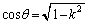 �C�@���A���̂Ƃ��A
�C�@���A���̂Ƃ��A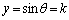 (
(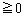 )
)
�܂�A�E�}�̓_D��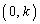 �ł��B
�ł��B
�@��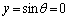 �Ƃ���ƁA
�Ƃ���ƁA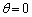 �C�B���A���̂Ƃ��A
�C�B���A���̂Ƃ��A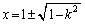
�܂�A�E�}�̓_A��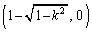 �C�_J��
�C�_J��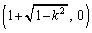 �ł��B
�ł��B
�@��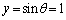 �Ƃ���ƁA
�Ƃ���ƁA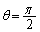 �C�B���A���̂Ƃ��A
�C�B���A���̂Ƃ��A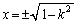
�܂�A�E�}�̓_B��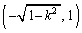 �C�_F��
�C�_F��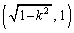 �ł��B
�ł��B
�ΐ����̋��E���̌�AD�́Axy���ʏ�̉~C���_P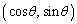 ��
��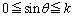 �ƂȂ�悤�ɓ����Ƃ��AP��x����������
�ƂȂ�悤�ɓ����Ƃ��AP��x����������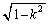 �������s�ړ��������_�̕`���Ȑ��Ȃ̂ŁAC
�������s�ړ��������_�̕`���Ȑ��Ȃ̂ŁAC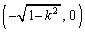 �𒆐S�Ƃ��锼�a1�̉~�ʂł��B���l�ɁA�E�}�̌�FJ�͉~��EI��x����������
�𒆐S�Ƃ��锼�a1�̉~�ʂł��B���l�ɁA�E�}�̌�FJ�͉~��EI��x����������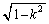 �������s�ړ��������Ȑ��ŁAH
�������s�ړ��������Ȑ��ŁAH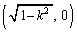 �𒆐S�Ƃ��锼�a1�̉~�ʂł��B
�𒆐S�Ƃ��锼�a1�̉~�ʂł��B
�܂��A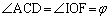 �Ƃ����ƁA
�Ƃ����ƁA
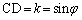 ����C �C
����C �C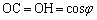
�f�ʐρA�����A�E�}�ΐ����̖ʐ�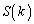 �́A��`HFJ�̖ʐ�(��`OEI�̖ʐ�)�A�����`OEFH�̖ʐς̘a����Ax��y���~��AD�ň͂܂��ʐ�(��`CAD�̖ʐς���O�p�`COD�̖ʐς�����������)�����������̂ɂȂ�܂��B
�́A��`HFJ�̖ʐ�(��`OEI�̖ʐ�)�A�����`OEFH�̖ʐς̘a����Ax��y���~��AD�ň͂܂��ʐ�(��`CAD�̖ʐς���O�p�`COD�̖ʐς�����������)�����������̂ɂȂ�܂��B
��`OEI�̖ʐς́A���a1�̉~�̖ʐς�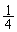 ��
��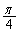 �C�����`OEFH�̖ʐς�
�C�����`OEFH�̖ʐς�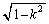 �C��`CAD�̖ʐς�
�C��`CAD�̖ʐς�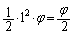
�O�p�`COD�̖ʐς�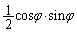
�� 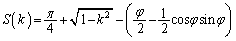 ����D
����D
���߂�̐�V�́A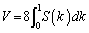
�D��φ ���܂ލ��́Ak�Őϕ����邱�Ƃ��ł��Ȃ��̂ŁA�C���A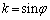 �Ƃ������u���ϕ����܂��B
�Ƃ������u���ϕ����܂��B
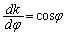 �C
�C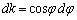 �Ck�F
�Ck�F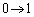 �̂Ƃ��Aφ�F
�̂Ƃ��Aφ�F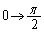
����āA
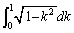 �́A
�́A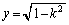 �Ƃ����ƁA
�Ƃ����ƁA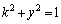 ���A���a1�̉~�̖ʐς�
���A���a1�̉~�̖ʐς�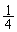 �ɓ������A
�ɓ������A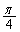
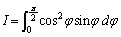 �́A
�́A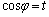 �Ƃ����ƁA
�Ƃ����ƁA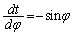 �C
�C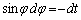 �Cφ�F
�Cφ�F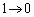
�� 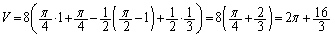 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B