���H�吔�w'06�N�O��[3]
���ʏ�a1��3�̉~�����L�̏���(a)��(b)�����Ȃ��瓮���Ƃ��A�����3�̉~�̘a�W���̖ʐ�S�̍ő�l�����߂�B
(a) 3�̉~�̒��S�͂��������_P�𒆐S�Ƃ��锼�a1�̉~����ɂ���B
(b) 3�̉~���ׂĂ����L����_��P�݂̂ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ȃ��A�O�p�`�̖ʐ��A�W���A2�~�̈ʒu�W�A�O�p�����Q�Ƃ��Ă��������B
����(b)���A3�̉~���ׂĂ����L���镔���̖ʐς�0�ł��B
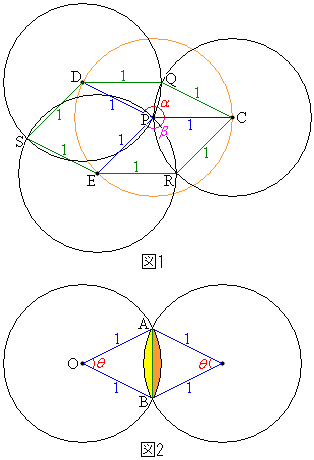
�]���āA3�̉~�̈ʒu�W�͉E�}1�̂悤�ɂȂ��Ă��āA3�̂���2���Ƃ��Ă���Ƌ��L���镔���̖ʐς͐��ł��B
2�̉~�����L���镔���̖ʐ�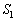 �́A�E�}2�̂悤�Ɋpθ ���Ƃ�ƁA��`OAB�̖ʐ�(��`�̖ʐςɂ��ẮA��ʊp���Q��)����O�p�`OAB�̖ʐς�������2�{���邱�Ƃɂ��A
�́A�E�}2�̂悤�Ɋpθ ���Ƃ�ƁA��`OAB�̖ʐ�(��`�̖ʐςɂ��ẮA��ʊp���Q��)����O�p�`OAB�̖ʐς�������2�{���邱�Ƃɂ��A
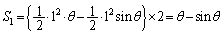 �@����@
�@����@
�Ƃ���ŁA3�̉~�̒��S��C�CD�CE�Ƃ��āA�E�}1�̂悤�ɁA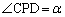 �C
�C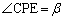 �Ƃ��܂��B���ɁA
�Ƃ��܂��B���ɁA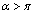 ���Ƃ���ƁAD��E�͒���CP�̓������ɗ��܂����A���̂Ƃ��A(b)�̏�������������Ȃ��Ȃ�܂��B����āA
���Ƃ���ƁAD��E�͒���CP�̓������ɗ��܂����A���̂Ƃ��A(b)�̏�������������Ȃ��Ȃ�܂��B����āA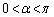 �ł��B���l�ɁA
�ł��B���l�ɁA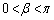 �ł��B�l�p�`CPDQ�Ǝl�p�`CPER�͂Ђ��`�ŁA
�ł��B�l�p�`CPDQ�Ǝl�p�`CPER�͂Ђ��`�ŁA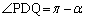 �C
�C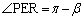
�@�ɂ����āA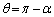 �Ƃ��āAC�𒆐S�Ƃ���~��D�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
�Ƃ��āAC�𒆐S�Ƃ���~��D�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
�@�ɂ����āA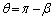 �Ƃ��āAC�𒆐S�Ƃ���~��E�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
�Ƃ��āAC�𒆐S�Ƃ���~��E�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
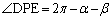 �C�l�p�`DPES�͂Ђ��`�ŁA
�C�l�p�`DPES�͂Ђ��`�ŁA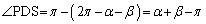
�@�ɂ����āA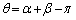 �Ƃ����āAD�𒆐S�Ƃ���~��E�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
�Ƃ����āAD�𒆐S�Ƃ���~��E�𒆐S�Ƃ���~�̋��L�����̖ʐς́A
����āA3�̉~�̘a�W���̖ʐ�S�́A3�̉~�̖ʐ�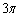 ���A2�Â��L����Ă��镔���̖ʐς������āA
���A2�Â��L����Ă��镔���̖ʐς������āA
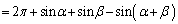
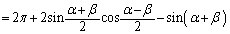 �@����A
�@����A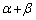 ���Œ肵(
���Œ肵(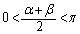 )�A
)�A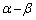 ���A
���A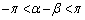 �͈̔͂œ������ƁA
�͈̔͂œ������ƁA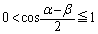 �C
�C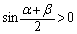 ���AS���ő�ƂȂ�̂́A
���AS���ő�ƂȂ�̂́A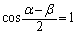 �C�܂�A
�C�܂�A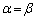 �̂Ƃ��B���̂Ƃ��A
�̂Ƃ��B���̂Ƃ��A
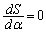 �Ƃ���ƁA
�Ƃ���ƁA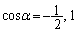
�� 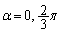
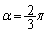 �̂Ƃ��A
�̂Ƃ��A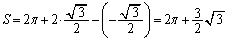
�����\���AS�̍ő�l�́A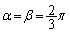 �̂Ƃ��A
�̂Ƃ��A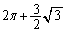 ......[��]
......[��]
�A�Ńg���b�L�[�Ȃ��Ƃ�����Ă���悤�Ɍ����܂����Aα�Cβ ��2�ϐ��̊�S�̍ő�ŏ����l����Ƃ��̏퓅��i�ł��B
2�ϐ��̂����̈���Œ肵���������āA�ő�E�ŏ����A�ŏ��ɌŒ肵���ϐ��̊��̌`�ɕ\���Ă����A����ɁA�ŏ��ɌŒ肵���ϐ������āA�ő�l�̍ő�l�A�ŏ��l�̍ŏ��l�����߂�̂����ʂł����A�����ł́AS��α�Cβ �Ɋւ��đΏ̂Ȍ`�����Ă���̂ŁA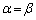 �̂Ƃ��ɍő�ɂȂ邾�낤�Ɨ\�������āA
�̂Ƃ��ɍő�ɂȂ邾�낤�Ɨ\�������āA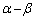 ���Ђ˂�o���悤�ɂ��܂��B
���Ђ˂�o���悤�ɂ��܂��B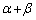 ��
��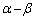 ��2�ϐ����̂悤�ɍl���A�܂��A
��2�ϐ����̂悤�ɍl���A�܂��A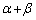 ���Œ肵��
���Œ肵��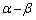 �����A�Ƃ����悤�ɍl���Ă��܂��B
�����A�Ƃ����悤�ɍl���Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B