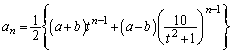���H�吔�w'10�N���[1]
a�Cb�Ct�͎����ŁA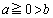 �Ƃ���B���̑Q�����ɂ��A����
�Ƃ���B���̑Q�����ɂ��A����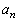 �C
�C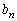 (
(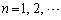 )���߂�B
)���߂�B
(1) 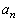 ��a�Cb�Ct�Cn��p���ĕ\���B
��a�Cb�Ct�Cn��p���ĕ\���B (2) 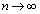 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A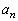 ���������邽�߂�a�Cb�Ct�ɂ��Ă̕K�v�\�����������߂�B
���������邽�߂�a�Cb�Ct�ɂ��Ă̕K�v�\�����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)���A���Q�����́A2�̑Q�����ŌW��������ւ���Ă��邾���A�Ƃ����ŕp�o�^�C�v�̂��̂ł��B���̃^�C�v�ł́A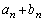 �C
�C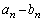 �����䐔��ɂȂ�܂��B
�����䐔��ɂȂ�܂��B
(2)�̋Ɍ��͈�Ђ˂�����Ă���̂Œ��ӂ��Ă��������B�Ȃ��A����̋Ɍ����Q�Ƃ��Ă��������B
(1) 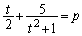 �C
�C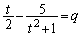 �Ƃ����ƁA
�Ƃ����ƁA 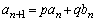 �@����@
�@����@
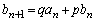 �@����A
�@����A�@�{�A���A
����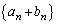 �́A����
�́A����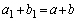 �C����
�C����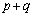 �����䐔���ł��B
�����䐔���ł��B ���A
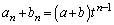 �@����B
�@����B�@�|�A���A
����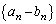 �́A����
�́A����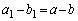 �C����
�C����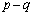 �̓��䐔��ł��B
�̓��䐔��ł��B ���A
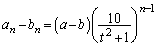 �@����C
�@����C�B�{�C���A
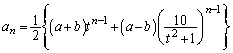 ......[��]
......[��]
(2) 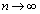 �̂Ƃ��A
�̂Ƃ��A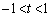 �ł����
�ł����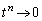 �C
�C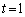 �ł����
�ł����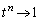 �C
�C ����ȊO��t�ɑ��ẮA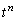 �͔��U���܂�(���䐔��̋Ɍ����Q��)�B
�͔��U���܂�(���䐔��̋Ɍ����Q��)�B
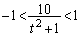 �ł����
�ł����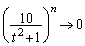 �C
�C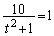 �ł����
�ł����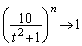 �C
�C
����ȊO�̏ꍇ�́A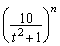 �͔��U���܂��B
�͔��U���܂��B
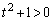 �Ȃ̂ŁA
�Ȃ̂ŁA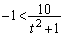 �ƂȂ�t�͑S�����ł��B
�ƂȂ�t�͑S�����ł��B ���������ƁA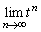 ��
��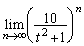 �̑o�����A�u�Ƃ��Ɏ�������v���Ƃ͂Ȃ��A�ƁA�킩��܂��B�Ƃ������Ƃ́A
�̑o�����A�u�Ƃ��Ɏ�������v���Ƃ͂Ȃ��A�ƁA�킩��܂��B�Ƃ������Ƃ́A (i) 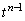 �̍�����������Ƃ��ɂ�
�̍�����������Ƃ��ɂ�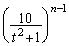 ���������Ȃ��̂ŁA
���������Ȃ��̂ŁA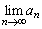 ���������邽�߂ɂ͌W��
���������邽�߂ɂ͌W��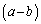 �̓[���ł���A
�̓[���ł���A (ii) 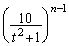 ����������Ƃ��ɂ�
����������Ƃ��ɂ�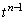 ���������Ȃ��̂ŁA
���������Ȃ��̂ŁA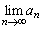 ���������邽�߂ɂ͌W��
���������邽�߂ɂ͌W��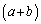 �̓[��
�̓[�� �Ƃ������Ƃł��B
�ł����A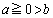 ���
���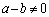 �Ȃ̂ŁA(i)�̏ꍇ�́A���蓾�܂���B(ii)���A
�Ȃ̂ŁA(i)�̏ꍇ�́A���蓾�܂���B(ii)���A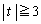 ����
���� 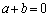 �̂Ƃ��ɁA
�̂Ƃ��ɁA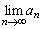 �͎������܂��B
�͎������܂��B
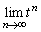 �����������A
�����������A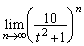 ���������Ȃ��Ƃ��ł����Ă��A
���������Ȃ��Ƃ��ł����Ă��A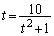 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A ���A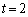 �ł����A
�ł����A �ƂȂ�A���̂Ƃ��ɂ��A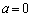 �ł���A
�ł���A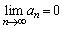 �ƂȂ�������܂��B
�ƂȂ�������܂��B
����ȊO�ɁA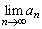 ����������ꍇ�͂���܂���B
����������ꍇ�͂���܂���B
�ȏ���A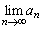 ���������邽�߂�a�Cb�Ct�ɂ��Ă��K�v�\�������́A
���������邽�߂�a�Cb�Ct�ɂ��Ă��K�v�\�������́A
�g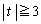 ����
���� 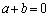 �h �܂��� �g
�h �܂��� �g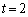 ����
���� 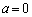 �h ......[��]
�h ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]