���H�吔�w'10�N�O��[1]
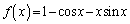 �Ƃ���B
�Ƃ���B
(1) 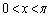 �ɂ����āA
�ɂ����āA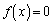 �͗B��̉��������Ƃ������B
�͗B��̉��������Ƃ������B (2) 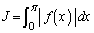 �Ƃ���B(1)�̗B��̉���α�Ƃ���Ƃ��AJ��
�Ƃ���B(1)�̗B��̉���α�Ƃ���Ƃ��AJ��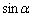 �̎��ŕ\���B
�̎��ŕ\���B (3) (2)�Œ�`���ꂽJ��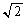 �̑召���r����B
�̑召���r����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����ڂ͂��ɂ������ł����A����čs���ƓT�^�p�^�[���������Ă��܂��B
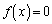 �Ƃ���ƁA
�Ƃ���ƁA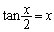 �@����@
�@����@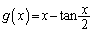
�Ƃ����ƁA
�����\���(���̑������Q��)�A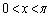 �ɂ����āA������
�ɂ����āA������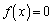 �C�����A
�C�����A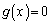 �́A(
�́A(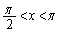 �͈̔͂�)�B��̉��������܂��B
�͈̔͂�)�B��̉��������܂��B
(2) 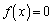 ��
��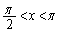 �ɂ������α�́A
�ɂ������α�́A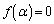 �C�����A�@���A
�C�����A�@���A 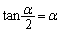 (
(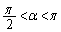 )�@����A
)�@����A�����܂��B
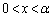 �ɂ����ẮA
�ɂ����ẮA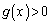 ���
���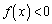 �C
�C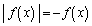
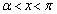 �ɂ����ẮA
�ɂ����ẮA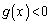 ���
���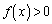 �C
�C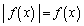 �@����B
�@����B
����āA �����ŁA
���A
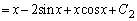 �@(
�@(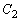 �F�ϕ��萔)
�F�ϕ��萔)����āA
(3) 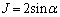 ��
��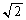 �̑召���ׂ�悢�̂ł����A2�Ŋ����āA
�̑召���ׂ�悢�̂ł����A2�Ŋ����āA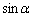 ��
��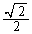 �̑召���ׂ邱�ƂɂȂ�܂��B�A���
�̑召���ׂ邱�ƂɂȂ�܂��B�A���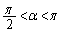 �C
�C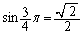 �Ȃ̂ŁA
�Ȃ̂ŁA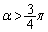 �Ȃ̂�
�Ȃ̂�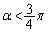 �Ȃ̂����킩��AJ��
�Ȃ̂����킩��AJ��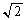 �̑召�f�ł��܂��B
�̑召�f�ł��܂��B α�́A�������@�̉��Ȃ̂ł����A(1)��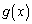 �̑����𗘗p����ƁA
�̑����𗘗p����ƁA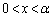 �ɂ�����
�ɂ�����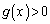 �C
�C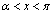 �ɂ�����
�ɂ�����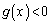 �Ȃ̂ŁA
�Ȃ̂ŁA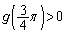 �ł����
�ł����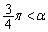 �ł���A
�ł���A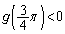 �ł����
�ł����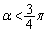 �ł��B
�ł��B
�ł����A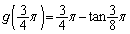 �ł́A
�ł́A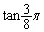 ������܂��B�B���A
������܂��B�B���A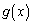 �̐�����
�̐�����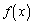 �̐������t�ɂȂ�̂ŁA
�̐������t�ɂȂ�̂ŁA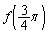 �ׂĂ݂܂��B
�ׂĂ݂܂��B ����āA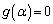 �C
�C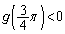 ���A(1)��
���A(1)��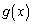 �̑����\����
�̑����\����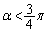
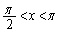 �ɂ�����
�ɂ�����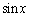 ���P�������Ȃ̂ŁA
���P�������Ȃ̂ŁA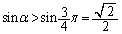
�� 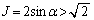 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B