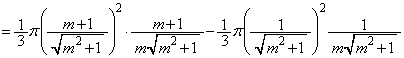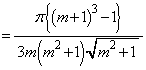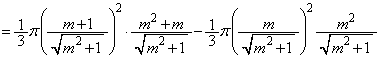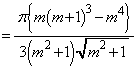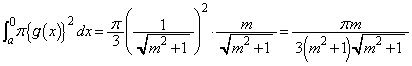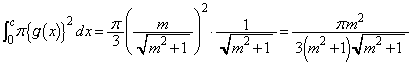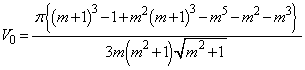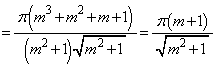���H�吔�w'11�N�O��[4]
���ʏ�Ɉ�ӂ̒�����1�̐����`D�����D�ƌ���钼��������Ƃ���B���̒���������D����]���ē������]�̂ɂ��Ĉȉ��̖₢�ɓ�����B
(1) D�Ɠ������ʏ�̒���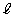 ��D�̂ǂ̕ӂɂ����s�łȂ����̂Ƃ���B���Ƃ��钼����
��D�̂ǂ̕ӂɂ����s�łȂ����̂Ƃ���B���Ƃ��钼����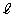 �ƕ��s�Ȃ��̂̒��ōl����Ƃ��A��]�̂̑̐ς��ő�ɂ��钼����D�ƗB1�_�Ō���邱�Ƃ������B
�ƕ��s�Ȃ��̂̒��ōl����Ƃ��A��]�̂̑̐ς��ő�ɂ��钼����D�ƗB1�_�Ō���邱�Ƃ������B (2) D�ƌ���钼�������Ƃ��Ăł��邷�ׂẲ�]�̂̑̐ς̒��ōő�ƂȂ�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł��B
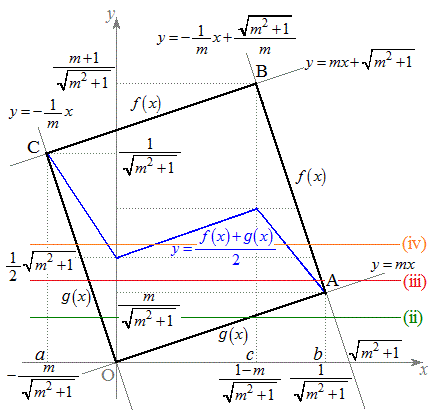 (1) �E�}�̂悤�ɁA����
(1) �E�}�̂悤�ɁA����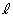 �ƕ��s��x���������A���_��1�����_O
�ƕ��s��x���������A���_��1�����_O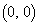 �ł���悤�ȁA1�ӂ̒���1�̐����`OABC���l���܂��B
�ł���悤�ȁA1�ӂ̒���1�̐����`OABC���l���܂��B����OA�̌X����m (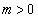 )�Ƃ��āA���̕������́A
)�Ƃ��āA���̕������́A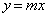 �@����@
�@����@
����BC�̕��������A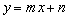 (
(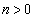 )�Ƃ��āA���_�ƒ���BC�Ƃ̋�����1�Ȃ̂ŁA
)�Ƃ��āA���_�ƒ���BC�Ƃ̋�����1�Ȃ̂ŁA 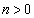 ���A
���A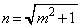
����BC�̕������́A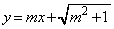 �@����A
�@����A
����OC�́A����BC�Ɛ����Ȃ̂ŁA����OC�̌X����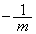 ��(�����̕��s�E�������Q��)�A���̕������́A
��(�����̕��s�E�������Q��)�A���̕������́A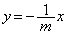 �@����B
�@����B
�A�C�B��A������ƁA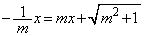 �C
�C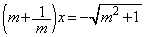
�� 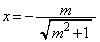 �C�B���A
�C�B���A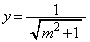
����āAC�̍��W��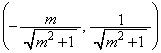
����AB�̕��������A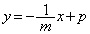 (
(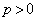 )�Ƃ��āA���_�ƒ���AB�Ƃ̋�����1�Ȃ̂ŁA
)�Ƃ��āA���_�ƒ���AB�Ƃ̋�����1�Ȃ̂ŁA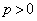 ���A
���A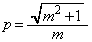
����AB�̕������́A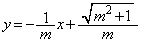 �@����C
�@����C
�@�C�C��A������ƁA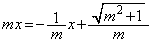 �C
�C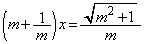
�� 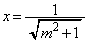 �C�@���A
�C�@���A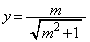
����āAA�̍��W��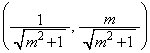
�A�C�C��A������ƁA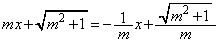
�� 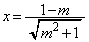 �C
�C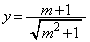
����āAB�̍��W��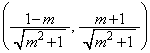
�����ŁA�}�`�̑��ݔ͈͂̍��[C��x���W��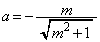 �C�E�[A��x���W��
�C�E�[A��x���W��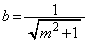 �Ƃ����܂��B
�Ƃ����܂��B
�܂��A��BC�C��AB��\������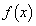 �C��OC�C��OA��\������
�C��OC�C��OA��\������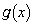 �Ƃ��܂��B�܂�A
�Ƃ��܂��B�܂�A
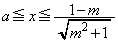 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A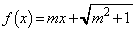
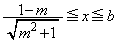 �̂Ƃ��A�C���A
�̂Ƃ��A�C���A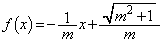
 �̂Ƃ��A�B���A
�̂Ƃ��A�B���A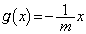
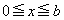 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A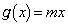
�����`OABC��y��������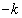 �������s�ړ�������x���̉��ɉ�]�����邱�Ƃɂ��A�����`D��
�������s�ړ�������x���̉��ɉ�]�����邱�Ƃɂ��A�����`D��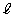 �ƕ��s�Ȓ����̂܂��ɉ�]������̂Ɠ���̏��l���邱�Ƃɂ��܂��B�܂�A
�ƕ��s�Ȓ����̂܂��ɉ�]������̂Ɠ���̏��l���邱�Ƃɂ��܂��B�܂�A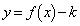 �C
�C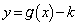 ��x���̉��ɉ�]������A�ƍl���܂��B
��x���̉��ɉ�]������A�ƍl���܂��B
�Ώ̐����Ak�ɂ��ẮA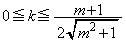 (
(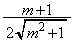 �́AB��y���W��
�́AB��y���W��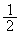 )�C�܂��Am�ɂ��ẮAC��y���W��A��y���W�����傫���Ȃ�͈́A
)�C�܂��Am�ɂ��ẮAC��y���W��A��y���W�����傫���Ȃ�͈́A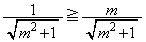 �C�܂�A
�C�܂�A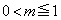 �͈̔͂ōl����Ώ\���ł��B
�͈̔͂ōl����Ώ\���ł��B 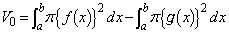 �@����D
�@����D(ii) 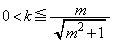 �̂Ƃ�(�E��}�ΐF��)�A
�̂Ƃ�(�E��}�ΐF��)�A ������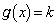 �́A
�́A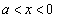 ��1������
��1������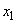 �C
�C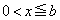 �͈̔͂�1������
�͈̔͂�1������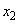 �������܂��B
�������܂��B
���̂Ƃ��A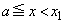 �C
�C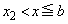 �ɂ����ẮA��]�̂�
�ɂ����ẮA��]�̂�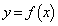 ����]�������̂���
����]�������̂���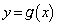 ����]�������̂���菜���Ηǂ��̂ł����A
����]�������̂���菜���Ηǂ��̂ł����A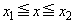 �ɂ����ẮA
�ɂ����ẮA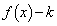 ��
��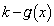 �̑傫��������]���邱�ƂɂȂ�܂��B
�̑傫��������]���邱�ƂɂȂ�܂��B
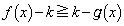 ���Ƃ���ƁA
���Ƃ���ƁA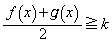
�����ŁA�E��̐}�ɁA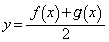 �̃O���t(�F��)�������Ă����܂����B���̃O���t�́A
�̃O���t(�F��)�������Ă����܂����B���̃O���t�́A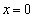 �̂Ƃ����
�̂Ƃ����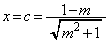 �̂Ƃ���Ő܂�Ȃ���܂��B
�̂Ƃ���Ő܂�Ȃ���܂��B
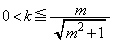 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�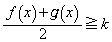 ���A
���A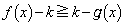 �Ȃ̂ŁA��]�̂̑̐�
�Ȃ̂ŁA��]�̂̑̐�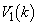 �́A
�́A 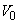 ��
��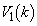 �̍����l���܂��B
�̍����l���܂��B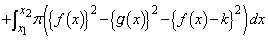
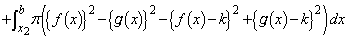 �@����E
�@����E�����ŁA�E�̂����A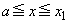 �C
�C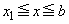 �ɂ������ϕ��̔�ϕ����ɂ��āA
�ɂ������ϕ��̔�ϕ����ɂ��āA 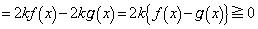 �@����F
�@����F����āA
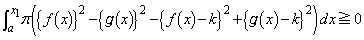 �@����G
�@����G
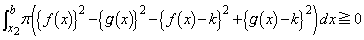 �@����H
�@����H�E�̂����A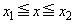 �ɂ������ϕ��̔�ϕ����ɂ��āA���͈̔͂ł́A
�ɂ������ϕ��̔�ϕ����ɂ��āA���͈̔͂ł́A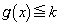 �Ȃ̂�
�Ȃ̂� 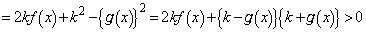 �@����I
�@����I����āA
����ƁA�G�C�H���A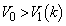 �@����J
�@����J (iii) 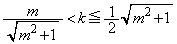 �̂Ƃ�(�E��}�ԐF��)�A
�̂Ƃ�(�E��}�ԐF��)�A ������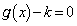 ��
��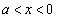 �͈̔͂�1������
�͈̔͂�1������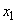 �������܂��B
�������܂��B
������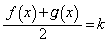 ��
��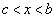 �͈̔͂�1������
�͈̔͂�1������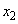 �������܂��B
�������܂��B
������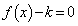 ��
��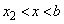 �͈̔͂�1������
�͈̔͂�1������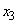 �������܂��B
�������܂��B
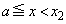 �ɂ����āA
�ɂ����āA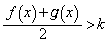 �C�܂�A
�C�܂�A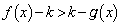
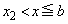 �ɂ����āA
�ɂ����āA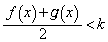 �C�܂�A
�C�܂�A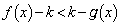
������A��]�̂̑̐�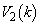 �́A
�́A ���̂����A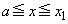 �C
�C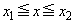 �ɂ������ϕ��̔�ϕ����́A�F�C�I�Ɠ��l�ɂ��āA0�ȏ�̒l���Ƃ�A�������u�P���I��0�v�ł͂Ȃ��̂ŁA
�ɂ������ϕ��̔�ϕ����́A�F�C�I�Ɠ��l�ɂ��āA0�ȏ�̒l���Ƃ�A�������u�P���I��0�v�ł͂Ȃ��̂ŁA �K��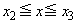 �ɂ������ϕ��̔�ϕ����ɂ��āA���͈̔͂ł́A
�ɂ������ϕ��̔�ϕ����ɂ��āA���͈̔͂ł́A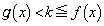 �Ȃ̂ŁA
�Ȃ̂ŁA 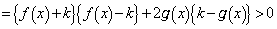 �@����L
�@����L�܂��A�K��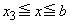 �ɂ������ϕ��̔�ϕ����ɂ��ẮA���͈̔͂ł�
�ɂ������ϕ��̔�ϕ����ɂ��ẮA���͈̔͂ł�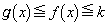 �ƂȂ�A
�ƂȂ�A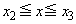 �̂Ƃ��Ɠ����悤�ɂ͍s���܂���B���̒�ϕ��́Am��0�ɋ߂�k��
�̂Ƃ��Ɠ����悤�ɂ͍s���܂���B���̒�ϕ��́Am��0�ɋ߂�k��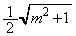 �ɋ߂��ƁA��ϕ��������ɂȂ邱�Ƃ�����܂��B
�ɋ߂��ƁA��ϕ��������ɂȂ邱�Ƃ�����܂��B
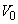 ��
��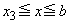 �ɂ������ϕ��́A
�ɂ������ϕ��́A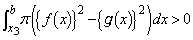 �Ȃ̂ŁA�K��
�Ȃ̂ŁA�K��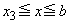 �ɂ������ϕ��ł́A
�ɂ������ϕ��ł́A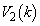 ��
��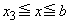 �ɂ������ϕ��́A
�ɂ������ϕ��́A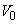 ��
��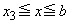 �ɂ������ϕ���������̂ł͂Ȃ��A
�ɂ������ϕ���������̂ł͂Ȃ��A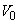 ��
��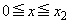 �ɂ������ϕ�����������Ƃɂ��܂�(����ǂ��Ƃ��납������̂ł͂Ȃ��A�]�T�̂���Ƃ��납�����)�B
�ɂ������ϕ�����������Ƃɂ��܂�(����ǂ��Ƃ��납������̂ł͂Ȃ��A�]�T�̂���Ƃ��납�����)�B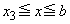 �ɂ����āA�K�̒�ϕ��̔�ϕ����̌��2���ɂ��āA
�ɂ����āA�K�̒�ϕ��̔�ϕ����̌��2���ɂ��āA 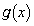 ��
��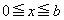 �ɂ����đ������Ȃ̂ŁAx��
�ɂ����đ������Ȃ̂ŁAx��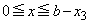 �Ƃ��āA
�Ƃ��āA���A
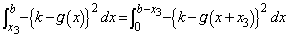 �@(�u���ϕ������Ă���)
�@(�u���ϕ������Ă���)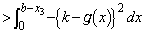 �@����M
�@����M�Ȃ̂ŁA�K��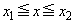 �̕����̒�ϕ��A
�̕����̒�ϕ��A 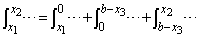 �@(
�@(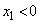 )
)�̂����̈ꕔ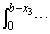 ����Ă��āA����ƇM�Ƃ̘a���Ƃ�ƁA
����Ă��āA����ƇM�Ƃ̘a���Ƃ�ƁA ���̔�ϕ����́A
���A
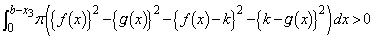 �@����N
�@����N���́A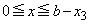 �Ƃ����ϕ��͈͂��A
�Ƃ����ϕ��͈͂��A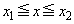 �̐ϕ��͈͂Ɋ܂܂�邩�A�Ƃ������Ƃł����A����AB�F
�̐ϕ��͈͂Ɋ܂܂�邩�A�Ƃ������Ƃł����A����AB�F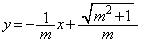 �ɂ�����
�ɂ�����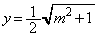 �Ƃ���ƁA
�Ƃ���ƁA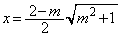 �ƂȂ�A
�ƂȂ�A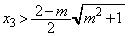 �ł����A
�ł����A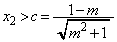 �Ȃ̂ŁA
�Ȃ̂ŁA ���A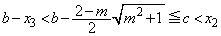 �ł����āA�ϕ��͈�
�ł����āA�ϕ��͈�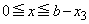 �͐ϕ��͈�
�͐ϕ��͈�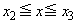 �Ɋ܂܂�܂��B�ȏ���A�K�́A
�Ɋ܂܂�܂��B�ȏ���A�K�́A �ȏ���A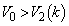
(iv) 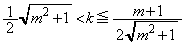 �̂Ƃ�(�E��}�̞�F��)�A
�̂Ƃ�(�E��}�̞�F��)�A ������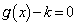 ��
��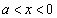 �͈̔͂�1������
�͈̔͂�1������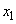 �������܂��B
�������܂��B
������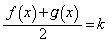 ���A
���A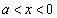 ��1������
��1������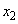 �C
�C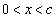 ��1������
��1������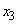 �C
�C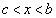 �͈̔͂�1������
�͈̔͂�1������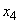 �������܂��B
�������܂��B
������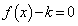 ��
��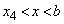 �͈̔͂�1������
�͈̔͂�1������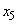 �������܂��B
�������܂��B
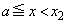 �C
�C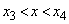 �ɂ����āA
�ɂ����āA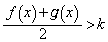 �C�܂�A
�C�܂�A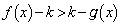
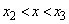 �C
�C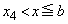 �ɂ����āA
�ɂ����āA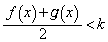 �C�܂�A
�C�܂�A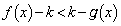
������A��]�̂̑̐�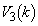 �́A
�́A ���̂����A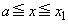 �C
�C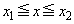 �C
�C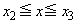 �C
�C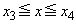 �C
�C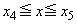 �ɂ������ϕ��̔�ϕ����́A�F�C�I�C�L�Ɠ��l�ɂ��āA0�ȏ�̒l���Ƃ�A�������u�P���I��0�v�ł͂Ȃ��̂ŁA
�ɂ������ϕ��̔�ϕ����́A�F�C�I�C�L�Ɠ��l�ɂ��āA0�ȏ�̒l���Ƃ�A�������u�P���I��0�v�ł͂Ȃ��̂ŁA �O��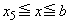 �ɂ������ϕ��́A(iii) ��
�ɂ������ϕ��́A(iii) ��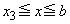 �ɂ������ϕ��Ɠ��l�ɁA��L�Ɠ����悤�ɂ͂����Ȃ��̂ŁA
�ɂ������ϕ��Ɠ��l�ɁA��L�Ɠ����悤�ɂ͂����Ȃ��̂ŁA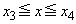 �ɂ������ϕ��ƍ��킹�čl���邱�ƂɂȂ�܂��B
�ɂ������ϕ��ƍ��킹�čl���邱�ƂɂȂ�܂��B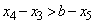 �C�܂��A
�C�܂��A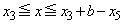 �Ƃ���
�Ƃ���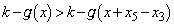 ���A�N�����̂Ɠ��l�ɂ��āA
���A�N�����̂Ɠ��l�ɂ��āA �� 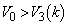
(i)�C(ii)�C(iii)�C(iv)���A��]�̂̑̐ς�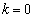 �̂Ƃ��ő�ŁA���Ƃ��钼����
�̂Ƃ��ő�ŁA���Ƃ��钼����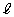 �ƕ��s�Ȃ��̂̒��ōl����Ƃ��A��]�̂̑̐ς��ő�ɂ��钼����D�ƗB1�_�Ō����܂��B
�ƕ��s�Ȃ��̂̒��ōl����Ƃ��A��]�̂̑̐ς��ő�ɂ��钼����D�ƗB1�_�Ō����܂��B
(2) (1)���Am���Œ肵�čl����Ƃ��A��]�̂̑̐ς̍ő�l�́A
���ꂼ��̒�ϕ��́A�~���A���邢�́A�~����̑̐ςƂ��āA
�����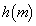 �Ƃ����ƁA
�Ƃ����ƁA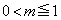 �ɂ����āA
�ɂ����āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 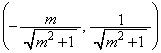
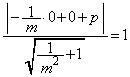
 �@(
�@(