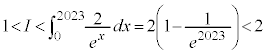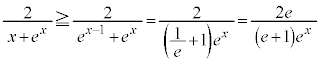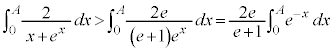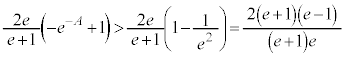���H�吔�w'23�N�O��[1]
����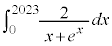 �̐������������߂�B
�̐������������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����A���̖�肪�ڂ��Ă�����W�̓������Ă��܂��ΈՖ�ł����A������ł͎肪���肪�Ȃ��A����ꓬ���邱�ƂɂȂ�܂��B���H��ł́A�͂��݂������p�o�Ȃ̂ŁA���R�A����1�ȓ��ɂȂ�悤��2���ł͂��ނ��Ƃ��l���܂��B�肪����̑S���Ȃ����Ȃ̂ŁA���j�͈ȉ��ȊO�ɂ��F�X�l�����܂��B
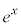 ���傫�Ȃ��̂͂Ȃ��̂ŁAx�̕���s�����ł͂��݂܂��B
���傫�Ȃ��̂͂Ȃ��̂ŁAx�̕���s�����ł͂��݂܂��B
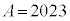 �C
�C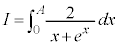 �Ƃ����ƁA
�Ƃ����ƁA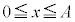 �ɂ����āA
�ɂ����āA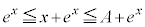 �C
�C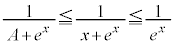
�����(��ϕ��ƕs�������Q��)�A
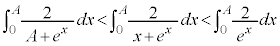 �@����@
�@����@
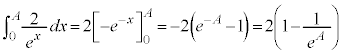 �@����A
�@����A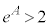 ���A
���A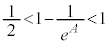 �ł����āA1�����傫��2������⏬�������ł��BI ��1�����傫���ƌ�����AI �̐���������1���Ƃ������ƂɂȂ�܂��B�@�̍��ӂ́A
�ł����āA1�����傫��2������⏬�������ł��BI ��1�����傫���ƌ�����AI �̐���������1���Ƃ������ƂɂȂ�܂��B�@�̍��ӂ́A
���̒��ŁA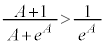 ���A
���A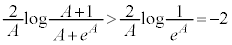 �Ƃ���̂ł́A�@���ӂ�0����Ƃ����������AI �̐���������0��1���m�肵�܂���B
�Ƃ���̂ł́A�@���ӂ�0����Ƃ����������AI �̐���������0��1���m�肵�܂���B
�@��I ��������������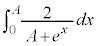 �Ƃ���̂ł͊ɂ�����̂ŁA���������傫�����̂��l����K�v������܂��B
�Ƃ���̂ł͊ɂ�����̂ŁA���������傫�����̂��l����K�v������܂��B
�����ŁA�ϕ���Ԃ��邱�Ƃ��l���܂�(��ϕ����Q��)�B
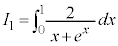 �C
�C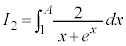 �Ƃ����܂��B
�Ƃ����܂��B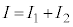 �ł��B
�ł��B
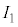 �̕��́A
�̕��́A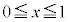 �ɂ����āA
�ɂ����āA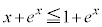 �C
�C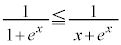
���̍��ӂ́A
����āA
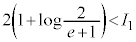 �@����B
�@����B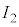 �̕��́A
�̕��́A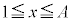 �ɂ����āA
�ɂ����āA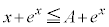 �C
�C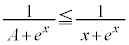
���̍��ӂ́A
�����ŁA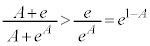 ���A
���A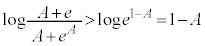 ���A
���A
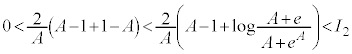 �@����C
�@����C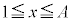 �ɂ�����
�ɂ�����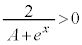 �Ȃ̂ŁA
�Ȃ̂ŁA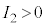 �ł��B
�ł��B
�B�{�C���A�C > 0�Ȃ̂�
�ƂȂ�̂ł����A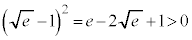 ���A
���A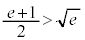 �C�܂�A
�C�܂�A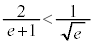 �Ȃ̂ŁA
�Ȃ̂ŁA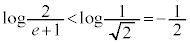 �ƂȂ�A
�ƂȂ�A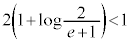 �ƂȂ��Ă��܂��A
�ƂȂ��Ă��܂��A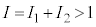 �������܂���B
�������܂���B
�����ŁA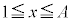 �̐ϕ��̔�r�Ώۂ̔�ϕ�����ʂ̊��ɕς��Ă݂܂��B
�̐ϕ��̔�r�Ώۂ̔�ϕ�����ʂ̊��ɕς��Ă݂܂��B
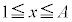 �ɂ����āA
�ɂ����āA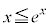 ���A
���A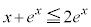
���́A���l�v�Z����ƁA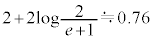 �C
�C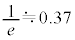 (������ł́A���d����g���킯�ɂ͍s���Ȃ��̂ŁA���̊m�F�͖����ł�)�ł����āA���̉E�ӂ�1�����傫���̂ŁA����łł��Ă���̂ł����A���d��Ȃ��ŁA�E�ӂ�1���傫�����Ƃ������̂��ɂ߂č���ł��B
(������ł́A���d����g���킯�ɂ͍s���Ȃ��̂ŁA���̊m�F�͖����ł�)�ł����āA���̉E�ӂ�1�����傫���̂ŁA����łł��Ă���̂ł����A���d��Ȃ��ŁA�E�ӂ�1���傫�����Ƃ������̂��ɂ߂č���ł��B
�����ŁA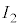 �̕��̐ϕ���Ԃ��������������Ă݂܂��B
�̕��̐ϕ���Ԃ��������������Ă݂܂��B
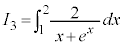 �C
�C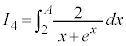 �C
�C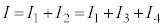 �ł��B
�ł��B
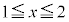 �ɂ����āA
�ɂ����āA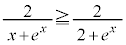 ���A
���A
�B���A
�����ŁA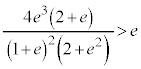 �ƂȂ��Ă����A
�ƂȂ��Ă����A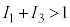 �ɂȂ�܂��B�����ŁAe��x�ɑウ�ĕ�������`���A
�ɂȂ�܂��B�����ŁAe��x�ɑウ�ĕ�������`���A
�Ƃ����āA���̋����ׂ܂��B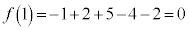 �Ȃ̂ŁA
�Ȃ̂ŁA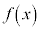 �������������āA
�������������āA
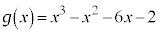 �Ƃ������������ƁA
�Ƃ������������ƁA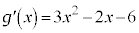 �C
�C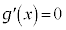 �Ƃ���ƁA
�Ƃ���ƁA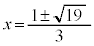 �C
�C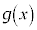 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B
�����\���A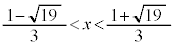 �ɂ�����
�ɂ�����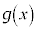 �͌����A
�͌����A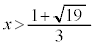 (
(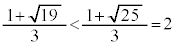 )�ɂ�����
)�ɂ�����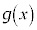 �͑����ł��B
�͑����ł��B
���A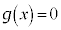 �C�܂�A
�C�܂�A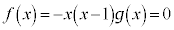 �́A
�́A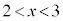 �͈̔͂ɂ͉����������A
�͈̔͂ɂ͉����������A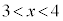 �͈̔͂ɉ��������܂��B�܂�A
�͈̔͂ɉ��������܂��B�܂�A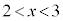 �͈̔͂�
�͈̔͂�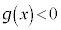 �C
�C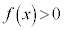 �ł��B
�ł��B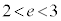 �Ȃ̂ŁA
�Ȃ̂ŁA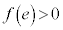 �C����āA
�C����āA
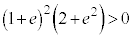 ���A
���A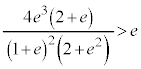 �@����D
�@����D
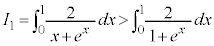 �C
�C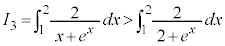 �C
�C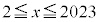 �ɂ�����
�ɂ�����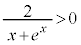 �ł�����
�ł�����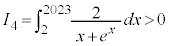 ���A
���A
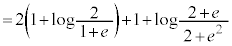
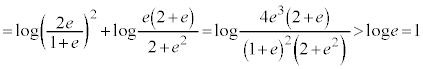 �@(�� �D)
�@(�� �D)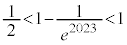 ���A
���A
����āA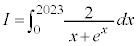 �̐���������1 ......[��]
�̐���������1 ......[��]
�ʉ��D��L�́A�ϕ���Ԃ�����ōs���A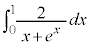 �C
�C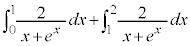 �C����Ǝ���ɑ傫���Ȃ��čs���̂ŁA�����͕K���ł�����S�m���ȕ��@�ł͂���܂����A�����ɂ���ςł��B
�C����Ǝ���ɑ傫���Ȃ��čs���̂ŁA�����͕K���ł�����S�m���ȕ��@�ł͂���܂����A�����ɂ���ςł��B �������Ŏ��s���낷�邤���ɁA����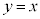 ���Ȑ�
���Ȑ�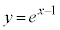 �̐ڐ��ł��邱�ƂɋC�Â���A�Ȑ�
�̐ڐ��ł��邱�ƂɋC�Â���A�Ȑ�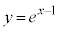 �͉��ɓʂȂ̂ŁA�ڐ�
�͉��ɓʂȂ̂ŁA�ڐ�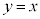 �͋Ȑ�
�͋Ȑ�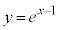 ���牺���ɂ���A���ׂĂ̎���x�ɂ��āA
���牺���ɂ���A���ׂĂ̎���x�ɂ��āA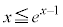 �ł��B������A
�ł��B������A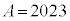 �Ƃ��āA
�Ƃ��āA 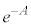 ��1�Ɣ�ׂĔ��ɏ��������ł����A
��1�Ɣ�ׂĔ��ɏ��������ł����A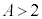 �Ȃ̂ŁA
�Ȃ̂ŁA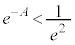 ���A
���A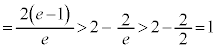 (��
(�� 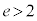 )
)��L�̇A�ƍ��킹�āA
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 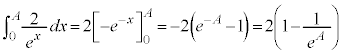 �@����A
�@����A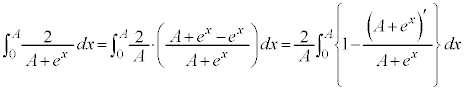
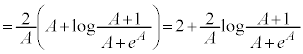
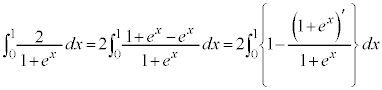
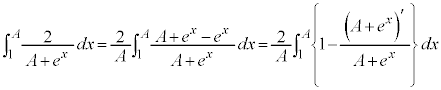
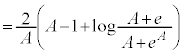
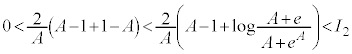 �@����C
�@����C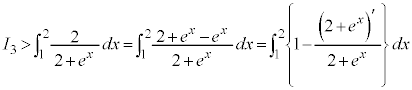
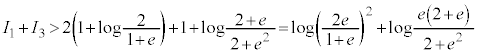
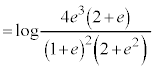
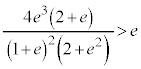 �ƂȂ��Ă����A
�ƂȂ��Ă����A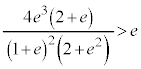 �@����D
�@����D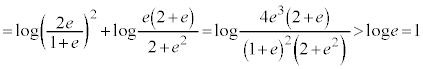 �@(�� �D)
�@(�� �D)