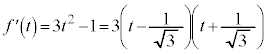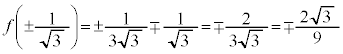���H�吔�w'23�N�O��[2]
������
���������̑g �����ׂċ��߂�B
�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������Ȃ�A�����ɕ�����܂����A�ǂ����Ă���ŗǂ��̂��A�ď�Ő�������_�q�͂�����܂��B�_�q��e�Ղɂ����@�̈�́A�Ȍ���_�킸�A���L�̂悤�ɁA������x�ꍇ���i���ăV���~�ׂ��ɂ��邱�Ƃł��B�Ȃ��������Q�Ƃ��Ă��������B
x�Cy�������Ȃ̂ŁA
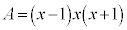 �C
�C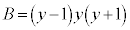 �@����@
�@����@
�A��3�����̐�A�CB�������l���Ƃ�Ƃ��A�����������x�Cy�����݂��邩�ǂ����ׂ邽�߂ɁA�����ŁAt ��3����
�̋����ׂĂ����܂��B��������ƁA
����āA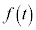 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B
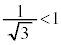 �Ȃ̂ŁA�����\���A
�Ȃ̂ŁA�����\���A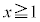 �ɂ�����
�ɂ�����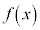 �͑������ł��B
�͑������ł��B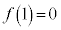 �Ȃ̂ŁA0�ȏ�̐���M�ɑ��āA������
�Ȃ̂ŁA0�ȏ�̐���M�ɑ��āA������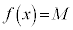 ��
��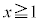 �͈̔͂ɁA������̉��������܂�(�����@�̕������ւ̉��p���Q��)�B�@���(��)
�͈̔͂ɁA������̉��������܂�(�����@�̕������ւ̉��p���Q��)�B�@���(��)
�^�����A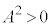 ���
���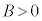 �ł����āAa�Cb�Cc�Cd�Ce�Cf��0�ȏ�̐����Ƃ��āA
�ł����āAa�Cb�Cc�Cd�Ce�Cf��0�ȏ�̐����Ƃ��āA
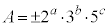 �C
�C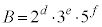 �@����A
�@����A
����āA
�B��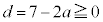 ���A
���A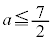 ��
��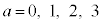 �Ɍ����܂��B
�Ɍ����܂��B
�C��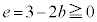 ���A
���A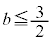 ��
��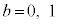 �Ɍ����܂��B
�Ɍ����܂��B
�D��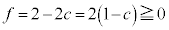 ���A
���A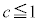 ��
��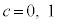 �Ɍ����܂��B
�Ɍ����܂��B
������A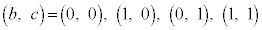 ��4�ʂ�ɕ����Ē��ׂ܂��B
��4�ʂ�ɕ����Ē��ׂ܂��B
(i) 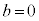 �C
�C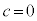 �̂Ƃ��A�A���
�̂Ƃ��A�A���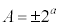 �ƂȂ�܂����AA��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł����A�s�K�ł��B
�ƂȂ�܂����AA��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł����A�s�K�ł��B (ii) 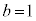 �C
�C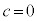 �̂Ƃ��A�C�C�D���
�̂Ƃ��A�C�C�D���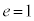 �C
�C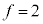 �ł��B�A���A
�ł��B�A���A 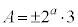 �C
�C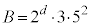 �@����E
�@����E�E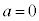 �̂Ƃ��A�E���
�̂Ƃ��A�E���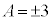 ��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł��܂���B
��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł��܂���B �E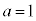 �̂Ƃ��A�E���
�̂Ƃ��A�E���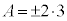 �́A
�́A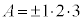 �C�܂�A
�C�܂�A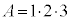 �܂���
�܂���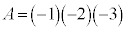 �̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B
�̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B ���̂Ƃ��@��x (�A��3�����̐^�̐�)�́A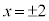 �C�B���
�C�B���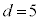 �C
�C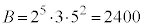 �ł����A
�ł����A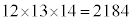 �C
�C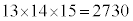 �ł����āA
�ł����āA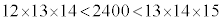 �Ȃ̂ŁA��L��(��)���A������
�Ȃ̂ŁA��L��(��)���A������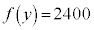 �̉��́A
�̉��́A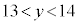 �͈̔͂ɂ���A
�͈̔͂ɂ���A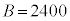 �͘A��3�����̐ςɂȂ邱�Ƃ͂���܂���B
�͘A��3�����̐ςɂȂ邱�Ƃ͂���܂���B �E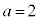 �̂Ƃ��AA���قȂ�3�����̐ςƂȂ�̂�
�̂Ƃ��AA���قȂ�3�����̐ςƂȂ�̂�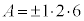 �C
�C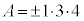 �̏ꍇ�݂̂ŁA
�̏ꍇ�݂̂ŁA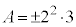 �́A�A��3�����̐ςƂȂ�܂���B�܂��́A
�́A�A��3�����̐ςƂȂ�܂���B�܂��́A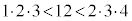 ���
���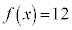 �̉��́A
�̉��́A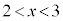 �͈̔͂ɂ����āA12��3�����̐ςŕ\�����Ƃ͂ł��Ȃ��A�Ƃ������܂��B
�͈̔͂ɂ����āA12��3�����̐ςŕ\�����Ƃ͂ł��Ȃ��A�Ƃ������܂��B �E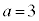 �̂Ƃ��A
�̂Ƃ��A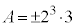 �́A
�́A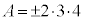 �C�܂�A
�C�܂�A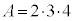 �܂���
�܂���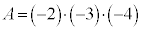 �̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B
�̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B ���̂Ƃ��@��x�́A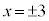 �C�B���
�C�B���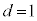 �C
�C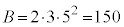 �ł����A
�ł����A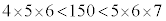 �Ȃ̂ŁA��L��(��)���A������
�Ȃ̂ŁA��L��(��)���A������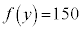 �̉��́A
�̉��́A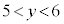 �͈̔͂ɂ���A
�͈̔͂ɂ���A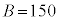 ���A��3�����̐ςɂȂ邱�Ƃ͂���܂���B
���A��3�����̐ςɂȂ邱�Ƃ͂���܂���B (iii) 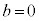 �C
�C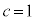 �̂Ƃ��A
�̂Ƃ��A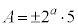 �ƂȂ�܂����AA��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł����A�s�K�ł��B
�ƂȂ�܂����AA��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł����A�s�K�ł��B (iv) 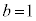 �C
�C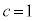 �̂Ƃ��A�C�C�D���
�̂Ƃ��A�C�C�D���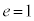 �C
�C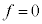 �ł��B
�ł��B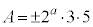 �C
�C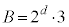 �ƂȂ�܂��B
�ƂȂ�܂��B �E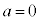 �̂Ƃ��A
�̂Ƃ��A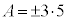 ��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł��܂���B
��6�̔{���łȂ��AA��A��3�����̐ςƂ��邱�Ƃ͂ł��܂���B �E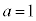 �̂Ƃ��A
�̂Ƃ��A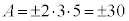 �ł́A
�ł́A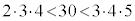 �Ȃ̂ŁA��L��(��)���A������
�Ȃ̂ŁA��L��(��)���A������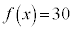 �̉��́A
�̉��́A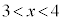 �͈̔͂ɂ���A
�͈̔͂ɂ���A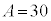 ���A��3�����̐ςɂȂ邱�Ƃ͂Ȃ��A�s�K�ł��B
���A��3�����̐ςɂȂ邱�Ƃ͂Ȃ��A�s�K�ł��B �E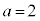 �̂Ƃ��A
�̂Ƃ��A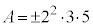 �́A
�́A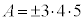 �C�܂�A
�C�܂�A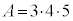 �܂���
�܂���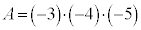 �̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B
�̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B ���̂Ƃ��@��x�́A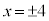 �C�B���
�C�B���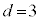 �C
�C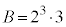 �ƂȂ�܂����A
�ƂȂ�܂����A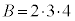 �̏ꍇ�̂ݘA��3�����̐ςɂȂ�A�@��y�́A
�̏ꍇ�̂ݘA��3�����̐ςɂȂ�A�@��y�́A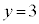 �ł��B
�ł��B �E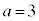 �̂Ƃ��A
�̂Ƃ��A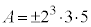 �́A
�́A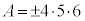 �C�܂�A
�C�܂�A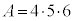 �܂���
�܂���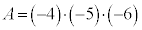 �̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B
�̂Ƃ��̂݁A�A��3�����̐ςƂȂ�܂��B ���̂Ƃ��@��x�́A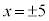 �C�B���
�C�B���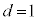 �C
�C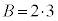 �ƂȂ�܂����A
�ƂȂ�܂����A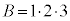 �̏ꍇ�̂ݘA��3�����̐ςɂȂ�A�@��y�́A
�̏ꍇ�̂ݘA��3�����̐ςɂȂ�A�@��y�́A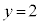 �ł��B
�ł��B
�ȏ���A���߂鐮���̑g�́A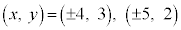 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B