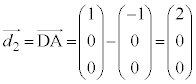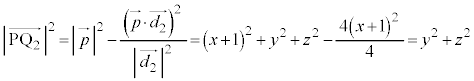���H�吔�w'23�N�O��[5]
xyz��Ԃ�4�_A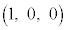 �CB
�CB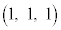 �CC
�CC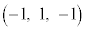 �CD
�CD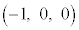 ���l����B
���l����B
(1) 2����AB�CBC���瓙�����ɂ���_�S�̂̂Ȃ��}�`�����߂�B
(2) 4����AB�CBC�CCD�CDA�ɋ��ɐڂ��鋅�ʂ̒��S�Ɣ��a�̑g�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�_�ƒ����̋����́A���̓_���璼���ɉ����������̒����ł��B(1)�ŁA2�������瓙�����ɂ���}�`�����߁A������g����(2)��4�����ɐڂ��鋅�ʂ����߂�̂ł����A(2)��(1)�Ɠ������Ƃ�2��J��Ԃ��̂ŁA(1)��v�̂悭����K�v������܂��B
 (1)
(1) 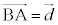 �C���߂�}�`��̓_��P
�C���߂�}�`��̓_��P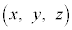 �C
�C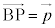 �Ƃ��܂��B�_P�ƒ���AB�Ƃ̋����́A�_P���璼��AB�ɐ���PQ�����낷�Ƃ�����PQ�̒����ł�(�����̃x�N�g�����������Q��)�B�_P��ʂ�
�Ƃ��܂��B�_P�ƒ���AB�Ƃ̋����́A�_P���璼��AB�ɐ���PQ�����낷�Ƃ�����PQ�̒����ł�(�����̃x�N�g�����������Q��)�B�_P��ʂ�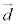 �ɐ����ȕ���π�ƒ���AB�Ƃ̌�_��Q�Ƃ���PQ�̒����ƌ������Ƃ��ł��܂��B
�ɐ����ȕ���π�ƒ���AB�Ƃ̌�_��Q�Ƃ���PQ�̒����ƌ������Ƃ��ł��܂��B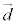 �͕���π�̖@���x�N�g���ł�(���ʂ̃x�N�g�����������Q��)�B
�͕���π�̖@���x�N�g���ł�(���ʂ̃x�N�g�����������Q��)�B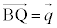 �Ƃ����ƁAQ�͒���AB��̓_�Ȃ̂ŁAk�������Ƃ��āA
�Ƃ����ƁAQ�͒���AB��̓_�Ȃ̂ŁAk�������Ƃ��āA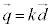 �@����@
�@����@�Ƃ������Ƃ��ł��܂�(�x�N�g����1���Ɨ����Q��)�B����π��̃x�N�g��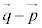 ���@���x�N�g��
���@���x�N�g��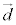 �ƒ������邱�Ƃ���A
�ƒ������邱�Ƃ���A �@��������ƁA
���D����́A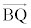 ��
��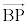 ��
��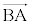 ��ւ̐��ˉe�ł��邱�Ƃ��Ӗ����Ă��܂��B�ŏ�����A���ˉe�ł���Ƃ��ĉ���Ό����I�ł��B
��ւ̐��ˉe�ł��邱�Ƃ��Ӗ����Ă��܂��B�ŏ�����A���ˉe�ł���Ƃ��ĉ���Ό����I�ł��B �u2����AB�CBC���瓙�����ɂ���_�v���l����̂ŁA�_P�ƒ���AB�Ƃ̋���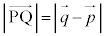 ���l���܂��B�A���A
���l���܂��B�A���A 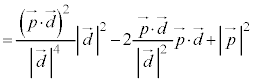
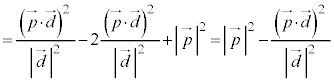 �@����B
�@����B�����ŁA���߂�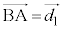 �C
�C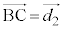 �Ƃ��AP���璼��BA�ɐ���
�Ƃ��AP���璼��BA�ɐ���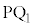 �CP���璼��BC�ɐ���
�CP���璼��BC�ɐ���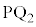 �����낷�ƁA�B���A
�����낷�ƁA�B���A 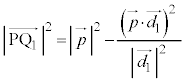 �C
�C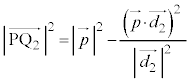 �@����C
�@����C�_P�ƁA����AB�C����BC�Ƃ̋������������̂ŁA�C��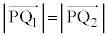 �Ƃ���
�Ƃ��� 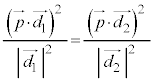 �@��
�@�� 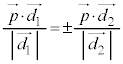 �@����D
�@����D���D����́A �Ƃ������Ƃł��B��
�Ƃ������Ƃł��B��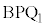 �Ɓ�
�Ɓ�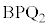 �ɂ����āABP���ʁA
�ɂ����āABP���ʁA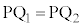 �C
�C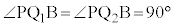 ���A��
���A��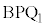 �߁�
�߁�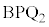 ��������̂ŁA��������A
��������̂ŁA��������A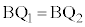 �Ƃ���A��L���������I�ɇD�������܂��B
�Ƃ���A��L���������I�ɇD�������܂��B
�ƂȂ�̂ŁA
�D�ɑ������ƁA
�����́{���Ƃ�ƁA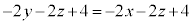 �@��
�@�� 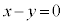 �@����F
�@����F
�����́|���Ƃ�ƁA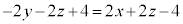 �@��
�@�� 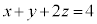 �@����G
�@����G
�F�C�G�́A���ʂ�\���܂��B�@����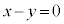 �ƕ���
�ƕ���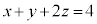 ......[��]
......[��]
(2) 4����AB�CBC�CCD�CDA�ɋ��ɐڂ��鋅�ʂ̒��S�́A4�����Ƃ̋��������ׂē������Ȃ�_�ł��B(1)��2����AB�CBC�Ƃ̋������������_���Ȃ��}�`(���ʁA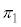 �Ƃ��܂�)�����߂��̂ŁA(1)�Ɠ��l�ɂ��āA2����BC�CCD�Ƃ̋������������_���Ȃ�����
�Ƃ��܂�)�����߂��̂ŁA(1)�Ɠ��l�ɂ��āA2����BC�CCD�Ƃ̋������������_���Ȃ�����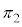 �A2����CD�CDA�Ƃ̋������������_���Ȃ�����
�A2����CD�CDA�Ƃ̋������������_���Ȃ�����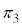 �A�����߂āA3���ʂ̌�_�����߂邱�ƂɂȂ�܂��B
�A�����߂āA3���ʂ̌�_�����߂邱�ƂɂȂ�܂��B (1)����L�̂悤�ɂ���Ȃ苁�߂�̂͗e�Ղł͂���܂��A(1)����Ԃ������ċ��߂��Ƃ��Ă��A�ʓ|�Ȏ菇������2��J��Ԃ����ƂɂȂ�̂ŁA(1)�̉��������悭�������āA����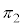 �C����
�C����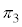 �ɂ��ẮA�D��p���Č����悭���߂�K�v������܂��B
�ɂ��ẮA�D��p���Č����悭���߂�K�v������܂��B
����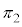 ��̓_P
��̓_P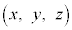 �ɂ��āA2����BC�CCD�Ƃ̋������l����̂ŁA�D�ŁAB��C�CA��B�CC��D�C
�ɂ��āA2����BC�CCD�Ƃ̋������l����̂ŁA�D�ŁAB��C�CA��B�CC��D�C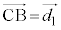 �C
�C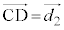 �CP���璼��CB�ɐ���
�CP���璼��CB�ɐ���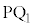 �CP���璼��CD�ɐ���
�CP���璼��CD�ɐ���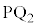 �����낷�Ƃ��āA
�����낷�Ƃ��āA �ƂȂ�̂ŁA
�D�ɑ������ƁA
�����́{���Ƃ�ƁA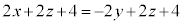 �@��
�@�� 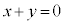 �@����I
�@����I
�����́|���Ƃ�ƁA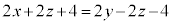 �@��
�@�� 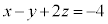 �@����J
�@����J
����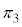 ��̓_P
��̓_P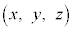 �ɂ��āA2����CD�CDA�Ƃ̋������l����̂ŁA�D�ŁAB��D�CA��C�CC��A�C
�ɂ��āA2����CD�CDA�Ƃ̋������l����̂ŁA�D�ŁAB��D�CA��C�CC��A�C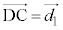 �C
�C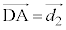 �CP���璼��DC�ɐ���
�CP���璼��DC�ɐ���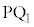 �CP���璼��DA�ɐ���
�CP���璼��DA�ɐ���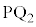 �����낷�Ƃ��āA
�����낷�Ƃ��āA �ƂȂ�̂ŁA
�D�ɑ������ƁA
�����́{���Ƃ�ƁA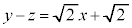 �@��
�@�� 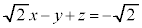 �@����L
�@����L
�����́|���Ƃ�ƁA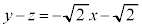 �@��
�@�� 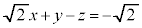 �@����M
�@����M
�����ŁA����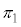 �C����
�C����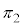 �C����
�C����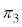 �̌�_(4�����Ɠ������ɂ���_�A�܂苅�ʂ̒��S)�����߂邱�ƂɂȂ�܂����A����
�̌�_(4�����Ɠ������ɂ���_�A�܂苅�ʂ̒��S)�����߂邱�ƂɂȂ�܂����A����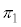 �͇F�܂��͇G�C����
�͇F�܂��͇G�C����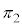 �͇I�܂��͇J�C����
�͇I�܂��͇J�C����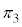 �͇L�܂��͇M�Ȃ̂ŁA���ʂ̒��S�́A
�͇L�܂��͇M�Ȃ̂ŁA���ʂ̒��S�́A �F�ƇI�ƇL�̌�_�A�F�ƇI�ƇM�̌�_�A�F�ƇJ�ƇL�̌�_�A�F�ƇJ�ƇM�̌�_
�G�ƇI�ƇL�̌�_�A�G�ƇI�ƇM�̌�_�A�G�ƇJ�ƇL�̌�_�A�G�ƇJ�ƇM�̌�_
��8�ʂ肠��܂��B���̊e�X�ɂ��ćC��p���āA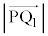 �C
�C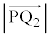 �����߂���ʂ̔��a�����߂���킯�ł����A�C�ɏo�Ă���A
�����߂���ʂ̔��a�����߂���킯�ł����A�C�ɏo�Ă���A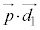 �C
�C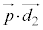 �����߂鎮�Ƃ��āA�E�C�H�C�K�̒��ŁA�ł��ȒP�ȇK�F
�����߂鎮�Ƃ��āA�E�C�H�C�K�̒��ŁA�ł��ȒP�ȇK�F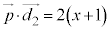 ���g�����Ƃɂ��܂��B���S�̍��W
���g�����Ƃɂ��܂��B���S�̍��W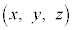 �ɑ��āA�K�ł́A
�ɑ��āA�K�ł́A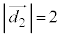 �C
�C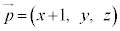 �Ȃ̂ŁA���a��2��́A
�Ȃ̂ŁA���a��2��́A �ƂȂ�A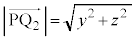 ���g���ċ��ʂ̔��a�����߂܂��B
���g���ċ��ʂ̔��a�����߂܂��B �L�̂Ƃ��A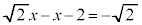 �C
�C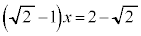 �C
�C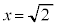 �C
�C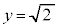 �C
�C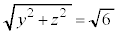
�M�̂Ƃ��A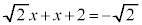 �C
�C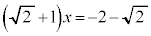 �C
�C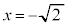 �C
�C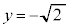 �C
�C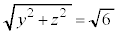
�L�̂Ƃ��A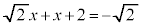 �C
�C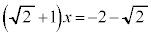 �C
�C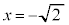 �C
�C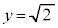 �C
�C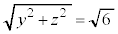
�M�̂Ƃ��A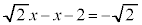 �C
�C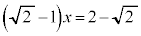 �C
�C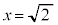 �C
�C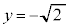 �C
�C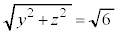
�E�G�|�J���A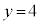 �C
�C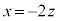
�L�̂Ƃ��A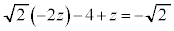 �C
�C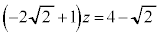 �C
�C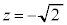 �C
�C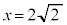 �C
�C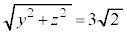
�M�̂Ƃ��A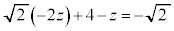 �C
�C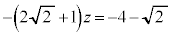 �C
�C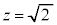 �C
�C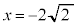 �C
�C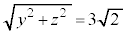
�ȏ���A���ʂ̒��S�Ɣ��a�́A
���S�F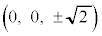 �C���a�F
�C���a�F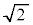
���S�F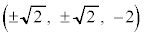 (��������)�C���a�F
(��������)�C���a�F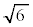
���S�F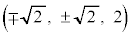 (��������)�C���a�F
(��������)�C���a�F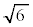
���S�F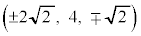 (��������)�C���a�F
(��������)�C���a�F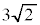 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 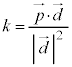 �C
�C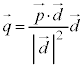 �@����A
�@����A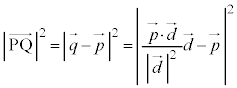
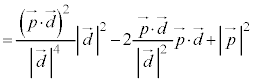
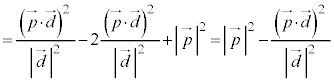 �@����B
�@����B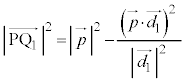 �C
�C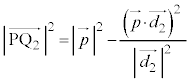 �@����C
�@����C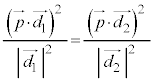 �@��
�@�� 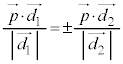 �@����D
�@����D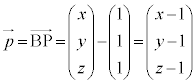 �C
�C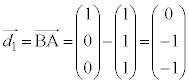 �C
�C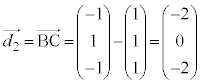
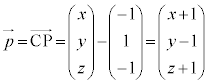 �C
�C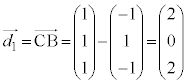 �C
�C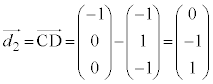
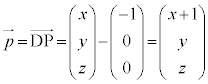 �C
�C �C
�C