東大理系数学'03年前期[5]
さいころをn回振り、第1回目から第n回目までに出たさいころの目の数n個の積を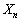
とする。
(1) 
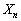が5で割り切れる確率を求めよ。 (2) 
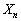が4で割り切れる確率を求めよ。 注意：さいころは1から6までの目が等確率で出るものとする。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率の基本的な問題ですが、場合分けのミスなどに注意が必要です。最後の極限のところでは、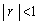
のとき、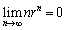
であることを使います。
(1) 
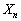が5で割り切れる ⇔ 第1回目から第n回目までに少なくとも1回5が出る
「少なくとも」という表現が出てくるので余事象の方を考えます。
「第1回目から第n回目までに少なくとも1回5が出る」という事象の余事象は、「第1回目から第n回目までに1度も5が出ない」という事象です。
さいころを1回振って5が出ない確率は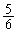
です。
これがn回続くので、第1回目から第n回目までに1度も5が出ない確率は、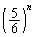
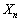が5で割り切れる確率は、
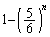......[答]
(2) これも(1)と同様に余事象を考えます。
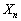が4で割り切れない
⇔ (i) 第1回目から第n回目まで、全て、1か3か5が出る、または、(ii) 第1回目から第n回目までの中で1回だけ2か6が出て、残りの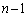
回は1か3か5が出る(i)を考えます。
さいころを1回振って1か3か5が出る確率は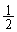
です。
これがn回続く確率は、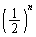
(ii)を考えます。2か6が出るのは、第1回目から第n回目までのどの回かが、
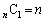通り。
さいころを1回振って2か6が出る確率は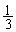
残りの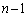
回、全て、1か3か5が出る確率は
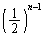(ii)の確率は、
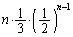(i)と(ii)は排反(和事象・積事象・余事象を参照)なので、求める確率、即ち、「(i)または(ii)」の余事象の確率は、
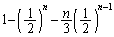......[答]
(3) これも余事象、「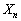
が20で割り切れない」という事象の方を考えます。余事象の確率は
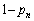です。
「
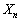が20で割り切れない」という事象は、
「
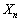が4で割り切れない」か「
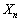が5で割り切れない」事象です。
「
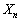が4で割り切れない」事象Aと「
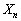が5で割り切れない」事象Bは、排反ではありません。
ともに、「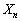
は4でも5でも割り切れない」という事象(
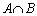)を共通に含んでいます。
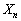は4でも5でも割り切れない
⇔ (i) 第1回目から第n回目まで、全て、1か3が出る、または、(ii) 第1回目から第n回目までの中で1回だけ2か6が出て、残りの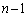
回は1か3が出る(i)の確率は、
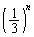(ii)の確率は、
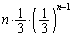(i)と(ii)は排反なので、
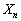が4でも5でも割り切れない確率は、 (2)より、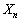
が4で割り切れない確率は、 (1)より、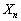
が5で割り切れない確率は、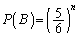
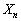が20で割り切れない(AまたはB)確率は、 極限をとるので、この中に出てくる、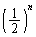
，
，
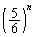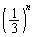の中で絶対値が最も大きいもの
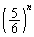でくくります。 ∴ 
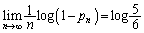......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
が20で割り切れる確率を
とおく。
を求めよ。
とすると、
，
より、