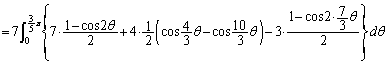���嗝�n���w'04�N�O��[3]
���a10�̉~C������B���a3�̉~��D���A�~C�ɓ��ڂ����Ȃ���A�~C�̉~���ɉ����Ċ��邱�ƂȂ��]�����B�~��D�̎���̈�_��P�Ƃ���B�_P���A�~C�̉~���ɐڂ��Ă���Ăщ~C�̉~���ɐڂ���܂łɕ`���Ȑ��́A�~C��2�̕����ɕ�����B���ꂼ��̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
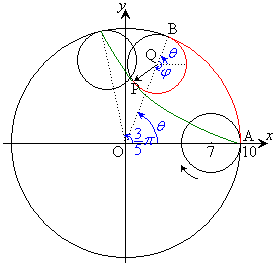 ���@P�͍ŏ��A�~C��̒�_A
���@P�͍ŏ��A�~C��̒�_A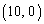 �ɂ����Ƃ��āA�����v���ɉ~C�̓�����]�����Ă����Ƃ��܂��B
�ɂ����Ƃ��āA�����v���ɉ~C�̓�����]�����Ă����Ƃ��܂��B
�~D�̒��S��Q�C�~C�Ɖ~D�̐ړ_��B�C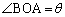 �C
�C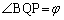 �Ƃ��܂��B
�Ƃ��܂��B
���ׂ邱�ƂȂ��]����̂ŁA�~��AB�̒���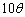 �Ɖ~��PB�̒���
�Ɖ~��PB�̒���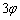 �͓������A
�͓������A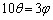 �@(��ʊp���Q��)
�@(��ʊp���Q��)
�� 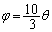
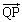 ��x���������ƂȂ��p�́A�����v���𐳂Ƃ��āA
��x���������ƂȂ��p�́A�����v���𐳂Ƃ��āA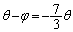
Q��O�𒆐S�Ƃ��锼�a7�̉~������܂��BQ�̍��W��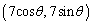 �C�����A
�C�����A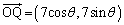 �@(�O�p�����Q��)
�@(�O�p�����Q��)
�� 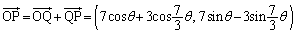
�_P�̍��W��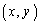 �Ƃ��āA
�Ƃ��āA
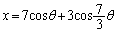 �C
�C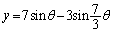 ����@
����@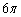 �Ɉ�v���܂��B
�Ɉ�v���܂��B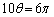
�� 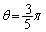
���̂Ƃ��́AB�̍��W��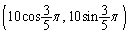
P��A���o�����čĂщ~C�̉~���ɐڂ���܂łɁAθ �́A0����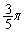 �܂œ����܂��B
�܂œ����܂��B
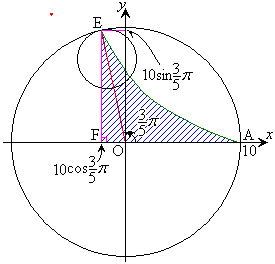 �E�}�ΐ����̖ʐς�S�Ƃ���ƁA
�E�}�ΐ����̖ʐς�S�Ƃ���ƁA
�@��p���āA�u���ϕ������܂��B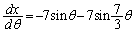 �C
�C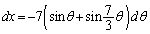 �Cx�F
�Cx�F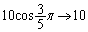 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F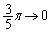
�� 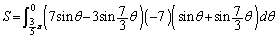
�����ŁA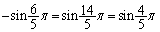 �C
�C �ł��B����āA
�ł��B����āA
���������̕����̖ʐς́A��`OAE�ƎO�p�`OEF�̖ʐς̘a����S�������悢�̂ŁA
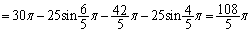 ......[��]
......[��]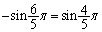 �ł�)
�ł�)
�傫�����̕����̖ʐς́A�~�̖ʐς��珬�������̖ʐς������āA
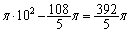 ......[��]
......[��]
�t�[�b�I��ςł��ˁB���ꂭ�炢�̔E�ϗ͂��Ȃ��Ăǂ�����A�ƁA����̐搶�͂�������肽���̂ł��傤����ǁA����I�ɂ́A�̗͂Ɏ��M�̂�����̔h�ȊO�̐l�́A�����������ăp�X�ł��ˁB���������̂ɂ������Ƒ�P�K�̂��Ƃł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B