���嗝�n���w '07 �N�O�� [3] ���W���ʏ�� 2 �_ P �C Q ���A�Ȑ� ( ������R�ɓ����Ƃ��A���� PQ �� 1 �F 2 �ɓ�������_ R �������͈͂� D �Ƃ���B�������A (1) a �� D �ɑ����邽�߂� b �̏����� a ��p���ĕ\���B (2) D ��}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� (1) 2 �_ P �C Q �̍��W�� PQ �� 1 �F 2 �ɓ�������_ R �̍��W�́A �C �@���A q ����������ƁA ��������ƁA
����A�@���A p ����������ƁA ��������ƁA
�� �@����B q �ɂ��Ă� 2 ���������������܂��B ���̃^�C�v�̖��ł́A�A�ƇB�������` �� 2 ���������ŁA 2 ���������� 2 ���� p �C q �Ȃ̂��A�Ƃ�����肪�����̂ł����A���̖��ł́A�����䂪 P �� Q �Ɋւ��đΏ̂ɂł��Ă��Ȃ� p �Ɋւ��� 2 ���������A�ƁA q �Ɋւ��� 2 ���������B���`���H������Ă��܂��܂� �B
2 �� 2 ���������̈Ӗ����l���Ă݂܂��B�_ R ��ʉ߂��钼���ƋȐ� 2 ��_�ł����Ƃ��āA R �� 2 ��_�����Ԑ����� 1 �F 2 �ɓ�������_�ł��B 2 ��_�̂��� R �ɋ߂����̓_�� P �C�������̓_�� Q �Ƃ��āA�A�� �_ P �� x ���W �����߂�
2 ���������A�B�� �_ Q �� x ���W �����߂�
2 ���������ɂȂ��Ă��܂��B R ���Ȑ���ɗ���ꍇ�́A ��ʉ߂��钼���� 0 �ȏ�ł� ( 2 ���������̈�ʘ_ ���Q�� ) �B �B�̔��ʎ��F �ǂ�����������ʂƂȂ�܂������A���̕s�����́A P �C Q ���Ȑ� PQ �� 1 �F 2 �ɓ�������_���A���̋Ȑ�����㑤 �ɂȂ���Ȃ�Ȃ����Ƃ��Ӗ����Ă��܂��B �C (i) �܂��A�E�} 2 �̂悤�ȏ��l����ƁA�_ R ��ʉ߂��钼���ƋȐ��Ƃ̌�_�� P �C Q �Ƃ��āA R �� PQ �� 1 �F 2 �ɓ�������ꍇ�� 2 �ʂ� ����A
���̂�������A P �C Q �͋Ȑ��� �ɗ��܂��B���̏�
(A) �Ƃ��܂��B (ii) �E�} 3 �̂悤�ȏ��l����ƁA R �� PQ �� 1 �F 2 �ɓ������A P �C Q �Ƃ��Ȑ��� 1 �ʂ� �ł��B���̂Ƃ��A
P �� x ���W p �ɂ��āA 2 �ʂ� �A
Q �� x ���W q �ɂ��āA 1 �ʂ� �ł��邱�Ƃɒ��ӂ��Ă��������B���̏�
(B) �Ƃ��܂��B �������A���̏ꍇ�A P �C Q �̂ǂ��炩�� y ���W�� R �� y ���W�ȉ��Ȃ̂ŁA P �̍��W p �ɂ��āA 1 �ʂ� �A
Q �̍��W q �ɂ��āA 1 �ʂ� �A�Ƃ������Ƃ͋N���肦�Ȃ����Ƃɂ����ӂ��Ă��������B
���������������ƌ����ƁA 2 ���������A�� P �C Q ���Ƃ��ɋȐ��� �̂ł��B
���ꂪ�A���̖��̃|�C���g�ł��B�P�Ȃ�u
2 ���������̉��̔z�u �v�̖��ł͂���܂���B ��蕶�̎w��ɓK����̂́A��L�� �� (A) �Ə� (B) �̏ꍇ
�� (A) �ɂ����ẮA 2 ���������A�C�B�Ƃ��ɁA 2 �̎����� �������܂��B
��
(B) �ɂ����ẮA 2 ���������́A ����� 2 �̎������������A������ 1 �̎����� �������܂�
( �Ƃ͌���Ȃ��̂ŁA�B�� 2 �̎����������ꍇ����������K�v������܂� ) �B�A�C�B���Ƃ��� 1 �̎����������A�Ƃ������Ƃ͂���܂���B R ���Ȑ���ɗ���Ƃ����܂߂�̂ŁA�u 2 �̎������v�̏ꍇ�ɂ͏d���̏ꍇ���܂݂܂��B ���Ɍ����悤�ɁA�A�C�B�Ƃ��A���������������́A p �� 2 ���������A���A 2 ������ �����̂́A
�Ƃ��āA
�C���A
�C���A
�C����āA
( 2 ���������̉��̔z�u ���Q�� ) ���A �� p �� 2 ���������A���A 1 ������ �����Ƃ��A
�C����āA
( ���Ԓl�̒藝 ���Q�� ) �� �@����E
q �� 2 ���������B���A 2 ������ �����̂́A
�Ƃ��āA
�C���A
�C���A
�C����āA
�� q �� 2 ���������B���A 1 ������ �����Ƃ��A
�C����āA
�� �@����G �� (A) �́A�C���D���F (B) �́A �g �C���D���G �h �C�܂��́A �g �C���E���F �h �����ŁA �g �C���E���F �h �����̂́A �g �C���D���F �h �̏ꍇ�Ɋ܂܂�܂��B ����āA���߂�����́A�C���D���g�F�܂��͇G�h
D ��}�������Ƃ��̋��E���́A
�@��� (a) �@��� (b) �@��� (c) �@��� (d) �@��� (e) ������A���߂�����́A ......[ �� ] (2) �̈� D ��}������ƁA�E�}�̉��ΐF���� ( ���E�����܂� ) �B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���嗝�n���w TOP �@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 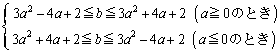 �@����E
�@����E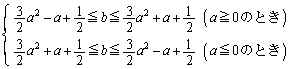 �@����G
�@����G