���嗝�n���w'09�N�O��[1]
���R��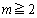 �ɑ��A
�ɑ��A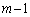 �̓W��
�̓W��
���l���A����炷�ׂĂ̍ő����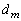 �Ƃ���B���Ȃ킿
�Ƃ���B���Ȃ킿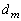 �͂���炷�ׂĂ������ő�̎��R���ł���B
�͂���炷�ׂĂ������ő�̎��R���ł���B
(1) m���f���Ȃ�A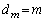 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) ���ׂĂ̎��R��k�ɑ��A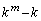 ��
��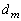 �Ŋ����邱�Ƃ��Ak�Ɋւ��鐔�w�I�A�[�@�ɂ���Ď����B
�Ŋ����邱�Ƃ��Ak�Ɋւ��鐔�w�I�A�[�@�ɂ���Ď����B (3) m�������̂Ƃ�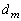 ��1�܂���2�ł��邱�Ƃ������B
��1�܂���2�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���嗝�n'97�N�O��[2](�قȂ�f��p�Cq�ɑ��A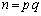 �Ƃ��āA
�Ƃ��āA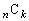 (
(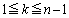 )�̍ő����1�ł��邱�Ƃ��������B
)�̍ő����1�ł��邱�Ƃ��������B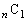 �C
�C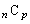 �C
�C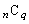 �ɒ��Ⴗ��)�Ɠ��l�̔��z�u
�ɒ��Ⴗ��)�Ɠ��l�̔��z�u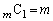 �ɒ���v������A(1)�͂����ł��B
�ɒ���v������A(1)�͂����ł��B
(2)�́Ak�Ɋւ������w�I�A�[�@�ł����āAm�Ɋւ��鐔�w�I�A�[�@�ł͂Ȃ��̂Œ��ӂ��Ă��������B
�Ȃ��A�������Q�Ƃ��Ă��������B
(1) m���f���̂Ƃ��A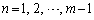 �Ƃ��āA
�Ƃ��āA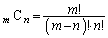 �̕��q�͑f��m���܂݁A����͑f��m���܂܂Ȃ��̂ŁA
�̕��q�͑f��m���܂݁A����͑f��m���܂܂Ȃ��̂ŁA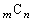 �́A���ׂ�m�Ŋ����܂��B
�́A���ׂ�m�Ŋ����܂��B ����A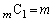 �͑f���Ȃ̂ŁA1��m�ȊO�̖������܂���B
�͑f���Ȃ̂ŁA1��m�ȊO�̖������܂���B
����āA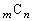 (
(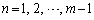 )�̍ő����
)�̍ő����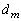 �́A
�́A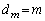 �ł��B
�ł��B
(2) (�T) 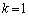 �̂Ƃ��A
�̂Ƃ��A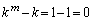 ��
��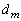 �Ŋ�����̂ŁA���藧���܂��B
�Ŋ�����̂ŁA���藧���܂��B (�U) 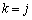 �̂Ƃ����藧�Ƃ���ƁA
�̂Ƃ����藧�Ƃ���ƁA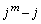 ��
��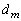 �Ŋ�����̂ŁAp�𐮐��Ƃ��āA
�Ŋ�����̂ŁAp�𐮐��Ƃ��āA 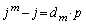 �@����@
�@����@�Ƃ������Ƃ��ł��܂��B�藝���A 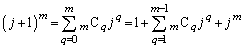 �@����A
�@����A�����ŁA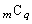 (
(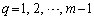 )�̍ő����
)�̍ő����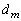 �ł����āA
�ł����āA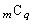 �͂��ׂ�
�͂��ׂ�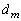 �̔{���Ȃ̂ŁAr�𐮐��Ƃ��āA
�̔{���Ȃ̂ŁAr�𐮐��Ƃ��āA 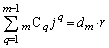 �@����B
�@����B�Ƃ������Ƃ��ł��܂��B����Ƈ@��p���ćA���A
�Ə����������Ƃ��ł��܂��B
�� 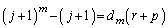 ������A
������A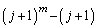 ��
��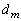 �Ŋ�����̂ŁA
�Ŋ�����̂ŁA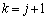 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B (�T)�C(�U)���A���ׂĂ̎��R��k�ɑ��A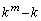 ��
��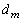 �Ŋ����邱�Ƃ�������܂���(���w�I�A�[�@���Q��)�B
�Ŋ����邱�Ƃ�������܂���(���w�I�A�[�@���Q��)�B
(3) (2)�Ɠ��l�ɍl���܂��B�藝���A
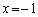 �Ƃ���ƁAm�͋����Ȃ̂ŁA
�Ƃ���ƁAm�͋����Ȃ̂ŁA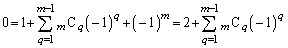 �@����C
�@����C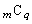 (
(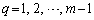 )�̍ő����
)�̍ő����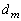 �ł����āA
�ł����āA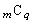 �͂��ׂ�
�͂��ׂ�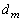 �̔{���Ȃ̂ŁAs�𐮐��Ƃ��āA
�̔{���Ȃ̂ŁAs�𐮐��Ƃ��āA�Ƃ������Ƃ��ł��܂��B����ƇC���A
������A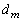 ��2�̐��̖ŁA1��2�Ɍ����܂��B
��2�̐��̖ŁA1��2�Ɍ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B