東京大学理系2009年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 自然数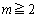
に対し、
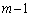個の二項係数
を考え、これらすべての最大公約数を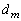
とする。すなわち
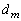はこれらすべてを割り切る最大の自然数である。
(1) mが素数ならば、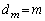
であることを示せ。 (2) すべての自然数kに対し、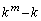
が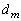
で割り切れることを、kに関する数学的帰納法によって示せ。 (3) mが偶数のとき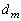
は1または2であることを示せ。 [解答へ]
[2] 実数を成分にもつ行列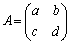
と実数r，sが下の条件(i)，(ii)，(iii)をみたすとする。
(i)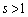 
(ii)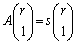 
このとき以下の問いに答えよ。
(1) 
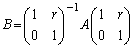をa，c，r，sを用いて表せ。 (3) 
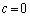かつ
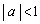を示せ。 [解答へ]
[3] スイッチを1回押すごとに、赤、青、黄、白のいずれかの色の玉が1個、等確率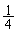
で出てくる機械がある。2つの箱LとRを用意する。次の3種類の操作を考える。
(A) 1回スイッチを押し、出てきた玉をLに入れる。
(B) 1回スイッチを押し、出てきた玉をRに入れる。
(C) 1回スイッチを押し、出てきた玉と同じ色の玉が、Lになければその玉をLに入れ、Lにあればその玉をRに入れる。
(1) LとRは空であるとする。操作(A)を5回おこない、さらに操作(B)を5回おこなう。このときLにもRにも4色すべての玉が入っている確率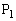
を求めよ。 (2) LとRは空であるとする。操作(C)を5回おこなう。このときLに4色すべての玉が入っている確率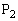
を求めよ。 (3) LとRは空であるとする。操作(C)を10回行う。このときLにもRにも4色すべての玉が入っている確率を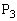
とする。
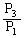を求めよ。 [解答へ]
[4] aを正の実数とし、空間内の2つの円板
を考える。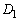
をy軸の回りに
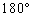回転して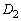
に重ねる。ただし回転はz軸の正の部分をx軸の正の方向に傾ける向きとする。この回転の間に
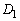が通る部分をEとする。Eの体積を
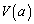とし、Eと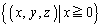
との共通部分の体積を
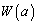とする。
(1) 
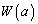を求めよ。 (2)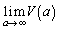 
を求めよ。 [解答へ]
[5](1) 実数xが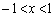
，
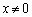をみたすとき、次の不等式を示せ。
(2) 次の不等式を示せ。
[解答へ]
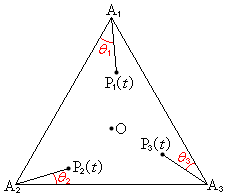[6] 平面上の2点P，Qの距離を
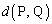と表すことにする。平面上に点Oを中心とする一辺の長さが1000の正三角形△
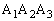がある。△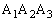
の内部に3点
，
，
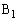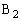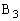を、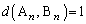
(
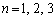)となるようにとる。また、
とおく。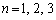
のそれぞれに対して、時刻0に
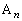を出発し、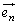
の向きに速さ1で直進する点を考え、時刻tにおけるその位置を
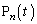と表すことにする。
(1) ある時刻tで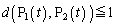
が成立した。ベクトル
と、ベクトル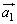
とのなす角度をθ とおく。このとき
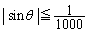となることを示せ。 (2) 角度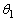
，
，
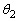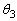を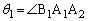
，
，
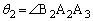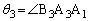によって定義する。αを
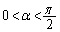かつ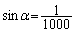
をみたす実数とする。(1)と同じ仮定のもとで、
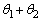の値のとる範囲をαを用いて表せ。 (3) 時刻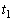
，
，
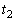のそれぞれにおいて、次が成立した。 このとき、時刻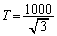
において同時に が成立することを示せ。
[解答へ]
各問検討
[1](解答はこちら) 雑誌「大学への数学」に掲載されている受験報告によると、この問題の(1)(2)は意外によくできているようです。パスカルの三角形を少し書いてみればよいのですが、「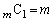
」には、東大受験生の多くが試験会場で気づけている、ということだと思います。
解答の最初のところに書いた京大理系'97年前期[2]：は次のような問題でした。
nが相異なる素数p，qの積、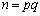
であるとき、
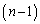個の数
(
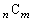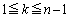)の最大公約数は1であることを示せ。
解答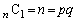 
なので、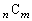
(
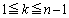)の最大公約数は、1かpかqか
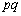です。
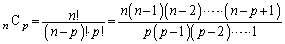では、分子のp個の整数の中に素数pの倍数は1個しかありません。また、分母には素数pが1個出てきます。従って、分母・分子でpが約されてしまい、分子には素数pの倍数は残らないので、
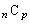はpの倍数ではありません。
また同様に、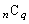
はqの倍数ではありません。
，･･･，
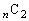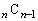の中に、pの倍数でないもの、qの倍数でないものが含まれるので、
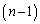個の数
(
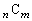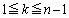)の最大公約数は1です。
この問題を考えたことがある人であれば、即座に「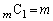
」を思いつけると思いますが、それほどポピュラーな問題とも言えないので、この問題を仮に知らなくても「
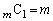」に気づかないようでは東大合格は難しい、ということだろうと思います。
もっと言うと、「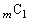
，
，･･･，
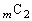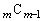」を見たときに、パスカルの三角形や、
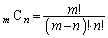，二項定理などが、頭に浮かぶようになっていて欲しいのです。これらは決して高級な受験技巧ではありません。教科書にも書かれていることです。東大合格(に限りませんが)のためには、まずは、教科書の基礎事項をしっかりとマスターしておくべきだ、ということが言えます。
「
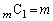」に着目できれば、(1)は、
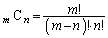の分母・分子に素数mが出てくるかどうか、ということだけです。
(2)の数学的帰納法は、解答にも書きましたが、問題文でことさらに「kに関する数学的帰納法」とことわっていることに注意できるか、ということに尽きます。出題者も心配になったのでわざわざ注意を喚起したのだろうと思います。「kに関する帰納法」ということになれば、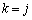
のときを仮定して
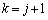のときを示すことになるので、
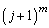に二項定理を適用するのは自然な流れになります。東大受験生の多くも、こうして解答したのだろうと思います。
(3)は、上記でも紹介した雑誌「大学への数学」に掲載されている受験報告によると、逆に、意外と不出来です。(2)で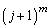
に二項定理を適用したら、jに数を、
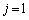とか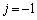
とかいろいろと入れてみる、ということ(微分したり積分したりしてから代入することだってあります)は、こうやれば必ず成功する、というものではありませんが、試験会場でもぜひ心がけてみて欲しいことです。
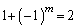を見た瞬間に、勝利を確信できるはずなのですが、(2)ができて(3)ができない、というのがやや残念な気がします。ちょっとしたイタズラ感覚なのですが、学校に便利な施設がいろいろとあるのに、いろいろと制約を付けて、せっかくの施設を宝の持ち腐れにしてしまっている学校が多くて、受験生が便利な式をいじってみようという気を起こさない、ということなのでしょうか？
[2](解答はこちら) 等比数列や極限などと融合されていて多少面倒な気はしますが、一筋に行列の計算をしていく問題で、こうした問題を落とさないことが、合格への必要条件です。
ここで使われている行列計算の技術は、積の計算、逆行列の計算、それに、行列の累乗を、2乗、3乗と計算することにより予測して帰納法で証明しておく、という程度の基本的なことです。行列の積の計算はミスをし易いところなので、しっかりと反復練習しておく必要があります。
東大前期でも、毎年、こうした基本的な出題が1題か2題あります。試験会場では、まず、6題をざっと見渡し、この基本問題から着手して調子に乗るのがよいと思います。
(1)の解答では、行列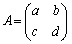
を2つの縦ベクトル
，
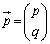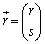にかける計算をするとき、これを1つにまとめる、という技巧を使っています。
という2式があるとき、この2式を1つにまとめて、
と書くことができます。
となっていることに注意してください。
また、(2)の解答では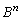
を求めてしまってから
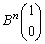を考えましたが、
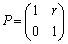として、
，
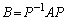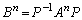なので、
より、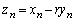
，
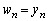から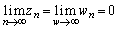
を示すこともできます。どうせ(3)で
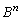の具体的な形を求める必要がありますが。
[3](解答はこちら) 昨年の確率の問題('08年前期[2])もそうですが、東大の確率の問題は、漸化式がからむ場合などを除いて易しいことが多い気がします。東大の出題者がどういう意図でそうしているのかはわかりませんが、東大前期の受験生は、最初に6題をざっと眺めて、確率から始めるのが良いように思います。易しいだけに、勘違いやケアレスや場合分け忘れをやってしまうと、命取りになってしまいます。最初に解答して最後の方で新鮮な気持ちで見直しをする、というのがミス対策になるでしょう。
本問'09年前期[3]は、玉の入り方を「同じものを含む順列」として考えることができれば、解答できます。「同じものを含む順列」は、n個のものがあるとき、そのうちのp個，q個、r個が同じであるとき(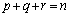
)の、n個のものの並べ方で、
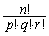通りあります。本問では、玉が4色あって、5個、あるいは、10個、出てきた順に並べるときに、4種類の同じものが(当然1つの種類については複数個ということが起こります)含まれることになります。
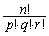は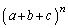
を展開したときの
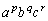の係数になります(多項定理)。多項定理で文字数を2文字にしたものが二項定理です。
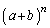を展開したときの
(
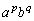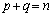)の係数は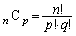
です。また、「同じものを含む順列」で種類を2種類にしたものが「組み合わせ」です。異なるn個のものからr個を選ぶ組み合わせ(
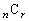通り)、というのは、n個のものを、「選ぶ」か「選ばない」かの2種類に分けながら並べる、と、見れば、「同じものを含む順列」ということになります。
単に教科書に載っている公式を棒暗記するのではなく、その奥に潜んでいる意味まで理解した上で、仮に試験場で公式をド忘れしてしまっても、その意味から引き出せるようにしましょう。
[4](解答はこちら) 本問の解答のところで、「積分計算に手を焼いて涙を飲んだ受験生も多いだろう」と書きましたが、[1]の検討でも参考にした、雑誌「大学への数学」の受験報告によると、本問の正答率は私の予想を超えるものだったようです。東大理系を狙う方は、まずは、この問題を自力で解けるようにすることを目標にして頂きたいと思います。
この問題の難しいポイントは2つあって、1つは、円板という変なものを回転させたときの通過領域の体積を求める、という点で、もう1つは、立体の体積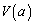
を定積分により求めようとすると積分計算で行き詰まる、という点です。(1)は前者、(2)は後者がポイントになっています。
雑誌「大学への数学」の受験報告を見ると、(1)は合格者の大半が正答に至っていて、(2)もかなりの合格者が「はさみうち」に気づいているようです。
(1)は、難関私大でも時々見られる問題で、参考書などにも記述がある技巧を用います。立体の断面に着目し、「変なもの」と断面との共通部分になる線分を回転させたときの通過領域を考えます。通過領域の面積は、線分と回転軸との距離の最大値を半径とする円の面積から最小値を半径とする円の面積を引いたものになり、この面積を回転軸に沿って積分すれば立体の体積を求めることができます。この技巧をマスターしていれば(1)は解答できます。
(2)は、技巧と呼べるものではなく、試験会場で危機的状況に陥ったときの臨戦的な実力が問われています。(2)を解答できるようにするためには、受験技巧を磨くことよりも、日頃から難問をじっくりと自分の頭で考え抜くことをどれだけやっているか、ということが大切なのです。
(1)はしっかり受験勉強しておけばできるはずの問題ですが、(2)は定積分の計算を続行するかどうか、他の方針に転換するかどうかの見極めが必要で、高度な状況判断力、意思決定の決断力、といったものが必要になります。つまり、東大合格のためには、まじめに勉強することはもちろんで、その上に、普通の人が見向きもしないような困難にも積極的に挑戦していく気力が求められるのです。東大を狙う方は、この辺を充分に意識してください。
じっくり考えるべき問題は、必ずしも数学の難問である必要はありません。複雑怪奇な推理小説の犯人捜しでもよいし、社会問題でもよいのです。少子高齢化の前に立ち行かなくなっている日本経済を打開するために新産業を起こす必要があるが、産業政策を進めると環境破壊も進んでしまう、というような二律背反的な問題、普通の高校生が見向きもしないような問題でも、図書館で本を借りてきてじっくり考えてみる、というような、一見、入試とは無関係に思われる努力が、入試会場で実を結ぶことがある、ということを、本問が教えてくれています。
受験生の皆さんが、将来、技術者、研究者として、社会の第一線に立つとき、ロボットの開発でも、磁気材料の開発でも、クリーン・エネルギーの開発でも、微細化技術の開発でも、最後の最後で、とても越えられそうもない二律背反的な難題が立ちはだかって頭を悩ませるような事態が必ず起こります。このとき、難題が解けそうもないから、ということで難題から逃避してしまえば、二流の技術者で終わってしまうでしょう。受験生のうちから、強い意志をもって困難にぶつかって行く気力を磨いておくように心がけましょう。
[5](解答はこちら) 多少場合分けも入りますが、自然対数を考え、不等式両辺の差を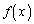
とおいて微分するだけの一本道の問題なのに、この問題は予想に反して出来が芳しくないようです。難問の[4]と[6]に挟まれて息切れしてしまった、ということかも知れませんが、'09年度の問題の中では、[3]に次いで取り易い問題ではないか、と、私は思うのです。'09年入試においては、[5]を確実にものにできた受験生が有利だった、ということが言えると思います。
この問題を落とした受験生は、恐らく、自然対数をとっただけの、
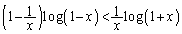
の形で、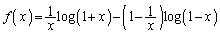
とおいて、微分して行ったのだろうと思われます。実は、かく言う私も、最初にそうしました。ですが、微分しても
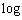が消えずに残ってしまうので、数分で、この方針ではだめだ、ということに気づけるはずです。[4]で力を使い果たして気持ちが焦ってしまうと、だめとわかっていても強行突破しようとして失敗しがちです。なので、'09年度の場合には、最初に[3]を手がけて次に[5]を抑え、[2]に飛んで3完を確保し、その後、[1]と[4]をゆっくりと熟考して得点を上積みする、という戦略で臨むべきです。[5]よりも先に[4]を手がけてしまうと[5]を取りこぼしやすくなる、ということです。東大を目指す方は、こうした点で、問題選択の目をしっかり養っておいて頂きたいと思います。
時間的に余裕のあるうちにこの問題に着手すれば、上記の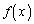
で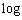
が残ってしまうのなら、xをかけてから微分してみてはどうか、という風に方針転換できるはずです。
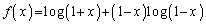とおけば、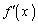
の形が悪くても、
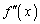まで計算すれば解決します。微分を複数回行う考え方は、
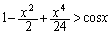の証明などでも出てくることなので、しっかり勉強してきた受験生であれば誰でも知っていることです。やはり、この問題は確実に得点しておくべき問題と言えるのではないでしょうか。
(2)は、(1)の結果で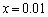
と代入するだけでは、不等式を示すことはできません。であれば、
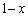とか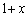
が出てくるので、ちょっと工夫し、
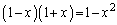を使って、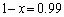
，
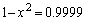とすればよい、というところまで、次から次へとアイデアをひねり出して行かなくてはなりません。この辺も、落ち着いて解答できるうちにこの問題を手がければ容易に思いつけるはずなのですが、時間的に切迫してしまうと、アイデアが湧いて来ない、ということになってしまいかねません。
試験会場での戦略の立て方も、合格する上での重要なポイントだということを意識するようにしましょう。
[6](解答はこちら) 試験会場で本問の問題文を目にした受験生は、「何じゃこりゃ」と思っただろうと思います。実際にやってみて、いやはや参りました。(1)，(2)はベクトルの基本に帰って考えれば何とかなるにしても、(3)まで完答できた受験生はほぼ皆無ではないかと思われます。数学オリンピックならともかく、こういう入試問題には、私は賛成しかねます。
想像するに、情報処理の基礎アルゴリズムなどを研究している出題者が、台風の進路予測や、社会的なパニック発生時の人間の行動の統計的シミュレーションを行うときに使う評価システムの処理を、焼き直して入試問題にした、という雰囲気です。ふだん、それを専門的に扱っている研究者にとっては当然と思えるような内容でも、初見の受験生にとっては驚愕し困惑するようなものでしかありません。
本問のような問題(かつての後期試験の問題もそうですが)は、未体験の状況に置かれたときの受験生の創意工夫の意欲を見ようというのが目的だと思います。とは言っても、全ての受験生にとって平等に新鮮に感じられるように、受験生にとって非日常的な環境を想定して試験を行うことで、果たして、受験生一人一人の真の実力を見極めることができるのでしょうか？私は、疑問符をつけたくなります。東大と言えども、もう少し、オーソドックスな問題で入学者選抜を行うのでよいのではないでしょうか。
さて、問題の方を見てみます。問題文の内容がかなりブッ飛んだ内容なのですが、こういう問題は逆に、基本に戻って基本に忠実に考えて行くべきです。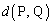
という記号が出てきて、理系'93年前期[3]や理系'94年前期[6](これも頭を抱え込んでしまう難問でした)を思い出しますが、
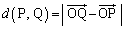ということでしかないので、高校数学をはみだすような発想をとらない、ということを肝に銘じてください。
この問題を全体を通して眺めてみると、正三角形の3頂点を出発して、本来なら、各角の2等分線の方向に進んだ3個の動点が中心で出会うはずなのに、それぞれが少しずれた方向に進んでしまったとしたら、中心付近でそのずれの大きさをどのように評価するか、ということがテーマになっています。
(1)では、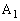
を出発した動点
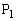と、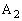
を出発した動点
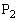との相対位置(
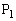から見た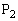
の位置)を表すベクトル
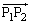の大きさ
(
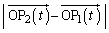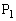と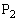
の距離)が小さければ、
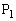から見た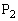
の相対速度の方向と、本来出会うはずの方向とのずれの角の正弦も小さくなることを示します。これは、ベクトル図を描きさえすれば、すぐにわかります。基本に帰れ、ということでしかありません。問題文に圧倒されて高校数学の知識からずれるようなことを始めると、時間だけがむなしく過ぎ去っていくことになります。
(2)では、本来出会うはずの方向に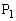
と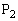
が進んでいけば、
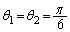になるはずなので、
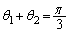になるはずです。ですが、(1)から
，
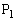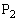の進む方向が、だいたい、
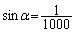となる角αぐらいずれているので、
，
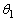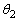もだいたいαぐらいずれるだろう、と、思えば、
，
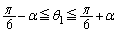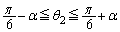より、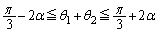
となるだろう、という予測ができます。ですが、問題文に描かれている図を見ていても、
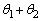がなかなか出てきません。ここは、(1)でベクトル図を描いてうまく行ったので、(2)もベクトル図を描くことにします。渦中にあるベクトルは、
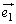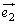と
と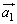
です。これで、解答の中の図の二等辺三角形DCEが描ければ、2つの底角が等しい、とすることによって、
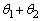が姿を現します。(1)を使って不等式を示すことができます。
問題の意図に順応するのに時間がかかると思いますが、ここまでは、やってできなくはない、と、思います。
(3)では、(1)の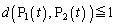
という条件が3種類出てくるので、
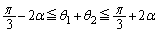も3種類出てきて、3つ足して
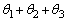の不等式を作り、
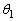の不等式：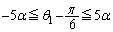
を作る、というところまでは、誰でも考えると思います。ですが、ここから、
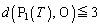，つまり、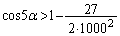
を示すのに大苦労をします。
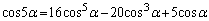を導き出すだけでも大変ですが、解答の注．に書いた、
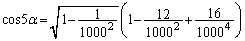と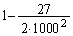
を2乗して引いて大小を比べる、ということになると、これだけでも、試験時間を超えてしまいます。従って、何らかの工夫が必要、ということになります。
他のウェブサイトを見ると、
から、
として、
･･･(＊)
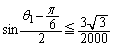より、
ここで、
とおいて、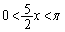
であれば
より、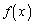
は単調増加で、
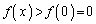より、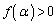
(明らかに、
)
∴ 
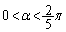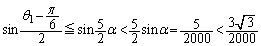
これで(＊)が成り立つので、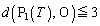
が成り立つ、ということになります。
確かに、この解法であれば、充分試験時間内に解答できると思います。きっと、これから、全国の予備校のスーパー東大コースなどというところで、この問題は、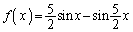
という関数を考えるんだ(これは、
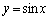のグラフが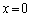
付近では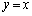
に非常に近い、ということを利用しているアイデアです)！東大受験は暗記だ！ということになるのかも知れません。ですが、幾多の入試問題を眺めているプロの予備校講師が解くのなら良いですが、高校3年間数学を学んだだけの受験生が、何のヒントもなしに、
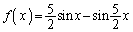を試験会場で思いつけるのでしょうかねえ？
いかに、エレガントな解法であっても、いかに美しい解法であっても、試験会場で思いつける解法でなければ、入試用の技巧としての意味がありません。予備校の授業で、頭脳明晰な講師が鮮やかに解くのを鑑賞して、受験生にどういうメリットがあるのか、私にはよくわかりません。本ウェブサイトでは、たとえ遠回りな解法であっても、まじめに高校3年間勉強してきた受験生が試験会場で思いつける解法を基本としています。
結局、この(3)は、入試会場では見もしないでパスする、というのが正解だと私は思います。パスするのが正解、という入試問題で良いのか、ぜひ、出題者には配慮をお願いしたいと、思います。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2023(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，･･･，
(
)とするとき、
(
)とするとき、
を示せ。
，
，
，
，
，
，
，
，
