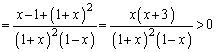���嗝�n���w'09�N�O��[5]
(1) ����x��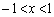 �C
�C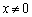 ���݂����Ƃ��A���̕s�����������B
���݂����Ƃ��A���̕s�����������B (2) ���̕s�����������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���s����͕K�v�ł����A��������v�Z���ē��_���Ă����������ł��B
(1)�́A�����Ȃ�(�E��)�|(����)�ł́A�w���̈������ʓ|�Ȃ̂őΐ����l���܂��B�Ȃ�ׂ��������₷���`�ɐ������܂��傤�B�Ȃ��A�����@�̕s�����ւ̉��p(2)���Q�Ƃ��Ă��������B
(1) �^�s�������ӂ����R�ΐ����l���Ă��s�����̌����͕ς��܂���B 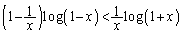 �@����@
�@����@�@�������悢�̂ł����A���̌`��(�E��)�|(����)�Ƃ��Ĕ��������log���c���Ė��ł��B�����ŁA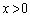 �C
�C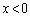 �ŏꍇ�������āAx�������������������Ƃɂ��܂��B
�ŏꍇ�������āAx�������������������Ƃɂ��܂��B (i) 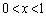 �̂Ƃ��A�@���ӂ�x��������ƁA
�̂Ƃ��A�@���ӂ�x��������ƁA 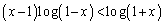 �@����A
�@����A���̏ꍇ�́A�ȉ��ŇA�����藧���Ƃ������܂��B
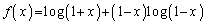 �@����B
�@����B�Ƃ����܂��B
����āA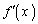 ���P�������ŁA
���P�������ŁA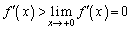
�]���āA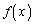 ���P�������ŁA
���P�������ŁA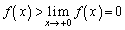
����āA�A�����藧���܂��B (ii) 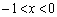 �̂Ƃ��A�@���ӂ�x��������ƁA
�̂Ƃ��A�@���ӂ�x��������ƁA 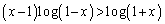 �@����C
�@����C���̏ꍇ�́A�ȉ��ŇC�����藧���Ƃ������܂��B
�B�̂悤��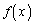 �������ƁA
�������ƁA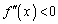
����āA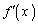 �͒P�������ŁA
�͒P�������ŁA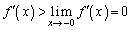
�]���āA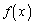 �͒P�������ŁA
�͒P�������ŁA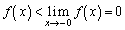
����āA�C�����藧���܂��B (i)�C(ii)���A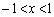 �C
�C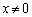 ���݂����Ƃ��A
���݂����Ƃ��A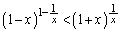 �����藧���܂��B
�����藧���܂��B
(2) ��蕶�̕s����
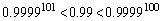 �@����D
�@����D�͔��ɂ���ǂ��s�����ɂȂ��Ă��āA�d��Ōv�Z���Ă݂��(������ł͂����͍s���܂���)�A
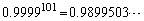 �C
�C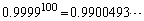
�ƂȂ��Ă��āA�e�G�ȕ]���ł͎����܂���B(1)�̕s�����𗘗p����ɂ��Ă��A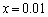 �Ƃ�
�Ƃ�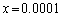 �C
�C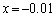 �C
�C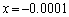 ��P�ɑ������̂ł́A�D�̌`����邱�Ƃ��ł��܂���B
��P�ɑ������̂ł́A�D�̌`����邱�Ƃ��ł��܂���B
�D�ɂ́A0.99��0.9999���o�Ă���̂ł����A 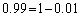 �C
�C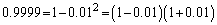
�ƂȂ�̂ŁA(1)�̕s������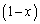 �ɂ�
�ɂ�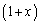 �������A
�������A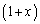 �ɂ�
�ɂ�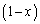 ��������
��������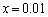 �Ƃ���Ƃ��܂��s�������ł��B
�Ƃ���Ƃ��܂��s�������ł��B
�����ŁA(1)�̕s�����̗��ӂ�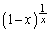 �������Ă݂܂��B
�������Ă݂܂��B 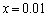 ��������ƁA
��������ƁA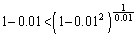
�� 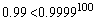 �@����E
�@����E
���ӂ̌`�ɍ��킹��(1)�̕s�����̗��ӂ�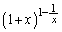 ��������ƁA
��������ƁA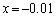 ��������ƁA
��������ƁA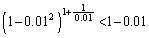
�� 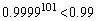 �@����F
�@����F
�E�C�F���A�D�������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B