���嗝�n���w'09�N�O��[6]
 ���ʏ��2�_P�CQ�̋�����
���ʏ��2�_P�CQ�̋�����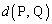 �ƕ\�����Ƃɂ���B���ʏ�ɓ_O�𒆐S�Ƃ����ӂ̒�����1000�̐��O�p�`��
�ƕ\�����Ƃɂ���B���ʏ�ɓ_O�𒆐S�Ƃ����ӂ̒�����1000�̐��O�p�`��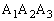 ������B��
������B��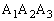 �̓�����3�_
�̓�����3�_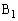 �C
�C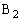 �C
�C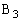 ���A
���A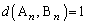 (
(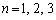 )�ƂȂ�悤�ɂƂ�B�܂��A
)�ƂȂ�悤�ɂƂ�B�܂��A
�Ƃ����B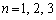 �̂��ꂼ��ɑ��āA����0��
�̂��ꂼ��ɑ��āA����0��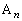 ���o�����A
���o�����A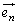 �̌����ɑ���1�Œ��i����_���l���A����t�ɂ����邻�̈ʒu��
�̌����ɑ���1�Œ��i����_���l���A����t�ɂ����邻�̈ʒu��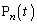 �ƕ\�����Ƃɂ���B
�ƕ\�����Ƃɂ���B
(1) ���鎞��t��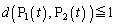 �����������B�x�N�g��
�����������B�x�N�g��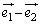 �ƁA�x�N�g��
�ƁA�x�N�g��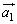 �Ƃ̂Ȃ��p�x��θ �Ƃ����B���̂Ƃ�
�Ƃ̂Ȃ��p�x��θ �Ƃ����B���̂Ƃ�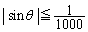 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (2) �p�x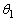 �C
�C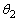 �C
�C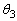 ��
��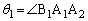 �C
�C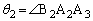 �C
�C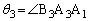 �ɂ���Ē�`����Bα��
�ɂ���Ē�`����Bα��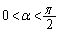 ����
����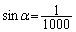 ���݂��������Ƃ���B(1)�Ɠ�������̂��ƂŁA
���݂��������Ƃ���B(1)�Ɠ�������̂��ƂŁA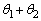 �̒l�̂Ƃ�͈͂�α��p���ĕ\���B
�̒l�̂Ƃ�͈͂�α��p���ĕ\���B (3) ����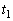 �C
�C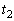 �C
�C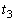 �̂��ꂼ��ɂ����āA�������������B
�̂��ꂼ��ɂ����āA�������������B ���̂Ƃ��A����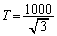 �ɂ����ē�����
�ɂ����ē����� ���������邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ă̌���������̖��ł����A�����������ł����x�N�g���̊�{������Ă��܂��B(1)�C(2)�͑�ӂ�c���ł������قǓ���͂���܂��A(3)�͐��l�����̕����ő���ȋC�́E�m�͂�K�v�Ƃ��܂��B
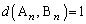 (
(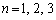 )���A
)���A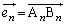 �͓��_�̈ړ������������P�ʃx�N�g���ŁA����0��
�͓��_�̈ړ������������P�ʃx�N�g���ŁA����0��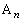 ���o�����A
���o�����A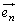 �̌����ɑ���1�Œ��i����_�̎���t�ɂ�����ʒu
�̌����ɑ���1�Œ��i����_�̎���t�ɂ�����ʒu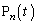 �������ʒu�x�N�g���́A
�������ʒu�x�N�g���́A
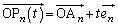 �@����@
�@����@
(1) 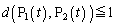 ���A
���A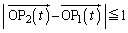 �ł��B�@���A
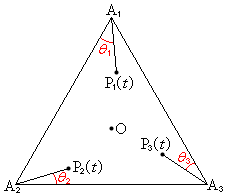
�ł��B�@���A ���̎��́A�E�}�̂悤�ɁA����0��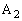 ���o���������_��
���o���������_��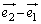 �̕����ɑ���
�̕����ɑ���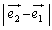 �Ői�݁A����t��
�Ői�݁A����t��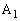 ����̋�����1�͈̔́A�܂�
����̋�����1�͈̔́A�܂�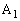 �𒆐S�Ƃ��锼�a1�̉~���ɗ��Ă���A�Ƃ������Ƃ��Ӗ����Ă��܂��B�E�}�ɂ����āA
�𒆐S�Ƃ��锼�a1�̉~���ɗ��Ă���A�Ƃ������Ƃ��Ӗ����Ă��܂��B�E�}�ɂ����āA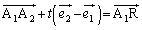 �Ƃ��āA
�Ƃ��āA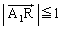 ���
���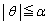
�� 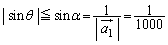
(2) ��蕶�̐}�߂Ă��Ă��A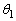 �C
�C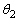 �̊W�͌����Ă��܂���B(1)�̌��ʂ́A
�̊W�͌����Ă��܂���B(1)�̌��ʂ́A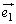 �C
�C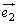 �͏���ȕ����������Ă���킯�ł͂Ȃ��A
�͏���ȕ����������Ă���킯�ł͂Ȃ��A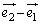 ��
��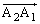 �ɂ��Ȃ�߂������������Ă���A�Ƃ������Ƃ��Ӗ����Ă��܂��B�܂�A
�ɂ��Ȃ�߂������������Ă���A�Ƃ������Ƃ��Ӗ����Ă��܂��B�܂�A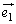 �C
�C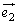 �̕����ɂ�
�̕����ɂ�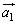 �̕����Ɋւ��ĉ��炩�̐�����̂ł����A��蕶�̐}�ł͂��ꂪ�c���ł��Ȃ��̂ł��B
�̕����Ɋւ��ĉ��炩�̐�����̂ł����A��蕶�̐}�ł͂��ꂪ�c���ł��Ȃ��̂ł��B 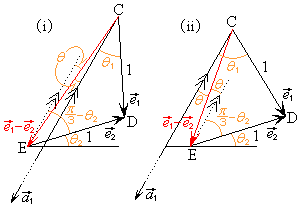 �����ŁA
�����ŁA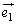 �C
�C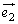 �C
�C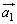 �������o�����x�N�g���}��`���Ă݂܂��B�E�}������ƁA
�������o�����x�N�g���}��`���Ă݂܂��B�E�}������ƁA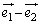 ��
��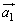 �̂Ȃ��p��θ�C
�̂Ȃ��p��θ�C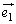 ��
��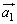 �̂Ȃ��p��
�̂Ȃ��p��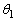 �Ȃ̂ŁA
�Ȃ̂ŁA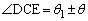 �ł��B�������{�ɂȂ�(�E�}(i))�Ƃ��A
�ł��B�������{�ɂȂ�(�E�}(i))�Ƃ��A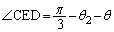 �C�������|�ɂȂ�(�E�}(ii))�Ƃ��A
�C�������|�ɂȂ�(�E�}(ii))�Ƃ��A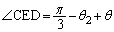 �ƂȂ�܂��B
�ƂȂ�܂��B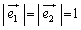 ���A�O�p�`DCE�͓ӎO�p�`�ŁA
���A�O�p�`DCE�͓ӎO�p�`�ŁA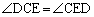 ���A
���A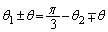 (��������)��
(��������)�� 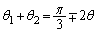
(1)���A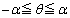 ���A
���A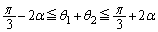 ......[��]
......[��]
(3) �����ׂ����A�Ⴆ�A
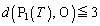 �́A����T�ɓ��_
�́A����T�ɓ��_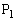 �͎O�p�`
�͎O�p�`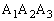 �̒��SO�̂��Ȃ�߂��ɂ��邱�Ƃ��Ӗ����Ă��܂��B����0���玞��
�̒��SO�̂��Ȃ�߂��ɂ��邱�Ƃ��Ӗ����Ă��܂��B����0���玞��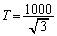 �܂ł̊Ԃɑ���1�œ��_���i�ދ����́A
�܂ł̊Ԃɑ���1�œ��_���i�ދ����́A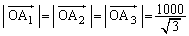 �ł��B�܂�A
�ł��B�܂�A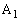 ���o������O�Ɍ������Đi�ނ̂ł�����傤��O�ɓ������鎞���ɁA���_
���o������O�Ɍ������Đi�ނ̂ł�����傤��O�ɓ������鎞���ɁA���_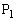 �͂�����Ƃ��ꂽ�����F
�͂�����Ƃ��ꂽ�����F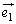 �̕����ɐi��ł���̂�O�ɂ͗��Ȃ������m��܂���O�̂��ɂ͗��Ă���A�Ƃ������Ƃł��B
�̕����ɐi��ł���̂�O�ɂ͗��Ȃ������m��܂���O�̂��ɂ͗��Ă���A�Ƃ������Ƃł��B�ƂȂ邱�Ƃ���A
�� 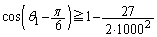 �@����A
�@����A
�ȉ��ł́A�A�����������Ƃ��ڕW�ɂȂ�܂��B
�Ƃ���ŁA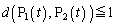 ����(2)�̌��ʂ�������̂ŁA
����(2)�̌��ʂ�������̂ŁA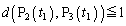 �C
�C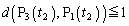 �C
�C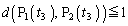 ��3������A
��3������A �������܂��B�����ŇC�{�D���A
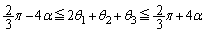 �@����E
�@����E�B�̊e�ӂɃ}�C�i�X�����ĕs�����̌�����ς��A
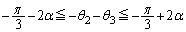 �@����F
�@����F�E�{�F���A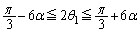
�� 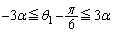 �@����G
�@����G ���D�������A(�B�{�C�{�D)��2���A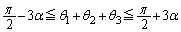 �@����H
�@����H �F�{�H���A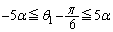
�Ƃ��Ă��܂��ƁA�G�����ɂ������ɂȂ��Ă��܂��A
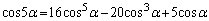 �@(
�@(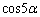 �̕ό`��
�̕ό`��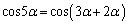 �𗘗p)
�𗘗p) �ƁA�A�E��(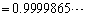 )�Ƃ̍����ɂ߂ď������A�A�������̂�����Ȃ�܂��B
)�Ƃ̍����ɂ߂ď������A�A�������̂�����Ȃ�܂��B
�G���A
���̉E�ӂƇA�̉E�ӂ��e�X2�悵�Ĕ�r����ƁA
�� 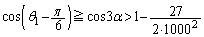 ����ćA�����藧�̂ŁA
����ćA�����藧�̂ŁA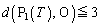 ���������܂��B
���������܂��B
���l�ɂ��āA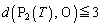 �C
�C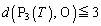 �����藧���܂��B
�����藧���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B