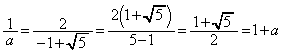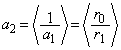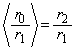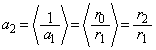���嗝�n���w'11�N�O��[2]
����x�̏����������A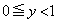 ����
����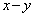 �������ƂȂ����y�̂��ƂƂ��A������L��
�������ƂȂ����y�̂��ƂƂ��A������L��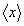 �ŕ\���B����a�ɑ��āA��������
�ŕ\���B����a�ɑ��āA��������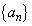 �̊e��
�̊e��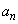 (
(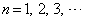 )�����̂悤�ɏ�����߂�B
)�����̂悤�ɏ�����߂�B
(i) 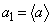
(ii) 
(1) 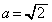 �̂Ƃ��A����
�̂Ƃ��A����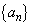 �����߂�B
�����߂�B (2) �C�ӂ̎��R��n�ɑ���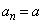 �ƂȂ�悤��
�ƂȂ�悤��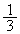 �ȏ�̎���a�����ׂċ��߂�B
�ȏ�̎���a�����ׂċ��߂�B (3) a���L�����ł���Ƃ���Ba�𐮐�p�Ǝ��R��q��p����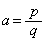 �ƕ\���Ƃ��Aq�ȏ�̂��ׂĂ̎��R��n�ɑ��āA
�ƕ\���Ƃ��Aq�ȏ�̂��ׂĂ̎��R��n�ɑ��āA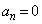 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ƃ����ɂ������Ȗ��ł����A���t���Ă݂����قǂł��Ȃ��A�Ƃ������ł��B(3)�͊���Z�̗]����g���čl���܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
(1) 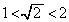 ���A
���A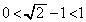
(ii)��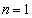 �Ƃ��āA
�Ƃ��āA 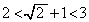 ���A
���A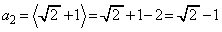
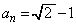 �ł���A
�ł���A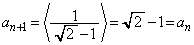
������A���ׂĂ̎��R��n�ɂ��āA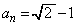
(2) (1)��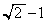 ��a��1�̌��ł��B
��a��1�̌��ł��B 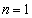 �̂Ƃ��A
�̂Ƃ��A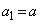 �ł��B(i)���
�ł��B(i)���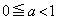 �ł���
�ł���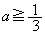 �Ȃ̂ŁA
�Ȃ̂ŁA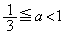 �@����@
�@����@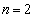 �̂Ƃ��A
�̂Ƃ��A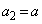 �ł����A(ii)���A
�ł����A(ii)���Ap�𐮐��Ƃ��āA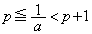 �Ƃ���ƁA
�Ƃ���ƁA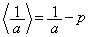 �C����āA
�C����āA �� 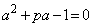
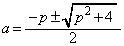 �@����A
�@����A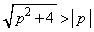 ���
���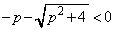 �Ȃ̂ŁA�@���A�A�̕����́{���Ƃ�A
�Ȃ̂ŁA�@���A�A�̕����́{���Ƃ�A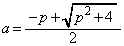 �@����B
�@����B�܂��A�@���A
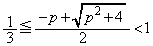
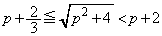 �@����C
�@����C�E���̕s�����ŁA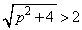 �C
�C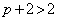 ���
���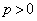
�C�̊e�ӂ�2�悷��ƁA �����̕s�������A
������A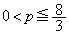 �ƂȂ�܂����A�����������p�́A
�ƂȂ�܂����A�����������p�́A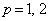
�B��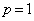 �Ƃ��āA
�Ƃ��āA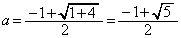
������A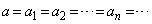
�B��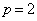 �Ƃ��āA
�Ƃ��āA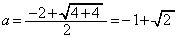
����́A(1)�����������܂��B
�ȏ���A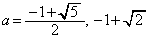 ......[��]
......[��] a��2��������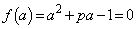 �́A
�́A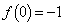 ���A���̉��ƕ��̉��������܂��B���̉���
���A���̉��ƕ��̉��������܂��B���̉���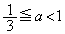 �͈̔͂ɑ��݂��邽�߂ɁA
�͈̔͂ɑ��݂��邽�߂ɁA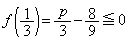 ����
���� 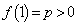 ��
�� 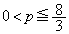
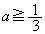 �Ƃ����������Ȃ���A�B�ŁA
�Ƃ����������Ȃ���A�B�ŁA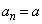 �ƂȂ邷�ׂĂ̎���a��^���܂��B
�ƂȂ邷�ׂĂ̎���a��^���܂��B
(3) p��q�Ŋ���Ƃ��̏���k (k�F����)�C�]���j (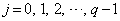 )�Ƃ��܂��B
)�Ƃ��܂��B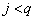 �ł��B
�ł��B 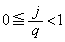 �Ȃ̂ŁA
�Ȃ̂ŁA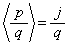 (i)���A
(i)���A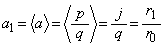
�����ŁA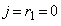 �Ȃ��(
�Ȃ��(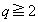 �ł������Ƃ��Ă�)�A
�ł������Ƃ��Ă�)�A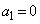 �C(ii)���A�ȍ~�A
�C(ii)���A�ȍ~�A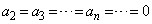
���ɁA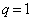 �Ȃ�
�Ȃ�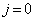 �C
�C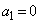 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ȍ�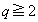 �Ƃ��āA
�Ƃ��āA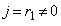 �Ȃ�A
�Ȃ�A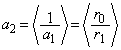
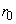 ��
��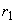 �Ŋ���Ƃ��̏���m (m�F����)�C�]���
�Ŋ���Ƃ��̏���m (m�F����)�C�]���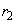 (
(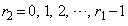 )�Ƃ��܂��B
)�Ƃ��܂��B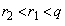 �ł��B
�ł��B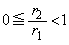 �Ȃ̂ŁA
�Ȃ̂ŁA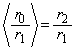
�ȍ~�A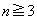 �̂Ƃ��A
�̂Ƃ��A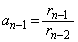 �Ƃ��āA
�Ƃ��āA
�����ŁA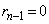 �ł����(
�ł����(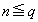 �ł������Ƃ��Ă�)�A
�ł������Ƃ��Ă�)�A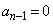 �C(ii)���A�ȍ~�A
�C(ii)���A�ȍ~�A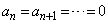
���ɁA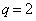 �Ȃ�
�Ȃ�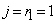 �ƂȂ�A
�ƂȂ�A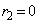 �C
�C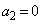 �ƂȂ�܂��B
�ƂȂ�܂��B
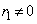 ����
����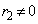 ���¥������
���¥������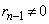 �ł���A
�ł���A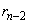 ��
��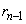 �Ŋ���Ƃ��̏���
�Ŋ���Ƃ��̏���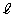 (
(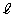 �F����)�C�]���
�F����)�C�]���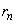 (
(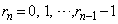 )�Ƃ��܂��B
)�Ƃ��܂��B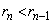 �ł��B
�ł��B 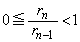 ���A
���A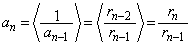
�������āA����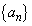 �C
�C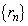 �����ƁA
�����ƁA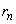 �C
�C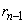 �C����C
�C����C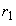 �Cq�͂������0�ȏ�̐����Ȃ̂ŁA
�Cq�͂������0�ȏ�̐����Ȃ̂ŁA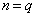 �ł���A
�ł���A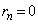 �C
�C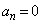
�ȍ~�A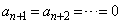
�ȏ���Aq�ȏ�̂��ׂĂ̎��R��n�ɑ��āA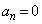
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B