東京大学文系2011年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] xの3次関数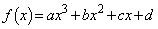
が、3つの条件
を全て満たしているとする。このような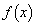
の中で定積分
を最小にするものを求め、そのときのIの値を求めよ。ただし、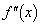
は
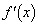の導関数を表す。
[解答へ]
[2] 実数xの小数部分を、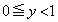
かつ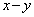
が整数となる実数yのこととし、これを記号
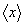で表す。実数aに対して、無限数列
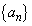の各項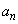
(
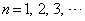)を次のように順次定める。
(i)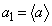 
(ii) 
(1) 
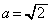のとき、数列
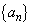を求めよ。 (2) 任意の自然数nに対して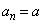
となるような
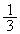以上の実数aをすべて求めよ。 [解答へ]
[3] p，qを2つの正の整数とする。整数a，b，cで条件
，
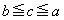
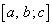の形に並べたものを
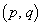パターンと呼ぶ。各
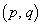パターン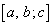
に対して
とおく。
(1) 
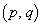パターンのうち、
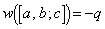となるものの個数を求めよ。また、
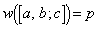となる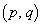
パターンの個数を求めよ。 以下、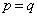
の場合を考える。
(2) sをp以下の整数とする。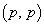
パターンで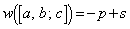
となるものの個数を求めよ。 [解答へ]
[4] 座標平面上の1点P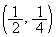
をとる。放物線
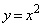上の2点Q
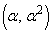，R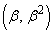
を、3点P，Q，RがQRを底辺とする二等辺三角形をなすように動かすとき、△PQRの重心G
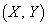の軌跡を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
