���嗝�n���w'11�N�O��[4]
���W���ʏ��1�_P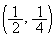 ���Ƃ�B������
���Ƃ�B������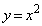 ���2�_Q
���2�_Q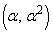 �CR
�CR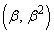 ���A3�_P�CQ�CR��QR���ӂƂ���ӎO�p�`���Ȃ��悤�ɓ������Ƃ��A��PQR�̏d�SG
���A3�_P�CQ�CR��QR���ӂƂ���ӎO�p�`���Ȃ��悤�ɓ������Ƃ��A��PQR�̏d�SG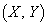 �̋O�Ղ����߂�B
�̋O�Ղ����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̐ݒ�͖ڐV�����ł����A�����͑Ώ̎��𗘗p����ÓT�I�Ȗ��ł��B�Ȃ��A���W���ʂɂ���������E�O�����Q�Ƃ��Ă��������B
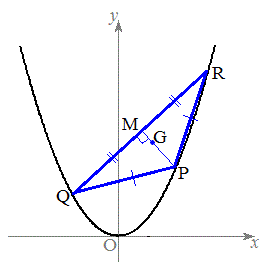 QR�̒��_M�́A
QR�̒��_M�́A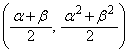
��PQR�̏d�SG��PM��2�F1�ɓ�������_�ŁA���̍��W�́A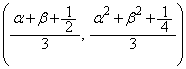
����āA
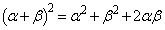 ���A
���A
�� 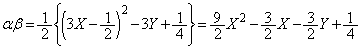
Q�CR�͈قȂ�2�_�ŁA�قȂ����α�Cβ �����݂��邽�߂ɁAα�Cβ ��2���Ƃ���x��2��������
�́A���قȂ�2�������������A����2���������̔��ʎ�D�ɂ��āA
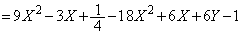
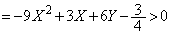 �@����A
�@����A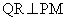 ���A
���A
����QR�̌X���́A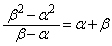
����PM�̌X���́A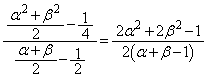
�@���A
�����ŁA�����A���l������ƁA�B���A
�ƂȂ�̂ŁA�A���A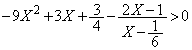
�� 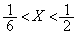 �@����D
�@����D
�C�C�D���A���߂��O���́A�Ȑ��F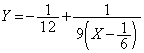 ��
��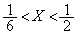 �̕����B ......[��]
�̕����B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 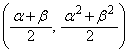
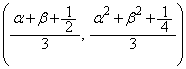
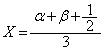 �C
�C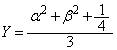
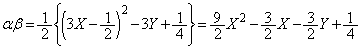
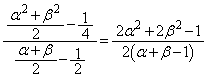
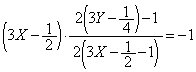
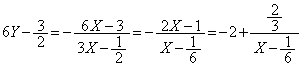 �@����B
�@����B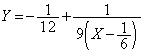 �@����C
�@����C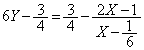
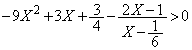
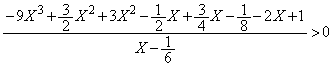
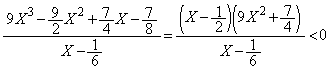
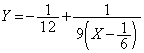 ��
��