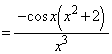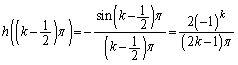東大理系数学'13年前期[2]
aを実数とし、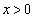 で定義された関数
で定義された関数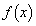 ,
,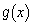 を次のように定める。
を次のように定める。
このとき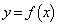 のグラフと
のグラフと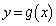 のグラフが
のグラフが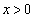 において共有点をちょうど3つ持つようなaをすべて求めよ。
において共有点をちょうど3つ持つようなaをすべて求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 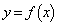 ,
,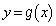 のグラフを追求していくと行き詰まります。文字定数は分離する(微分法の方程式への応用(2)を参照)、という定石であっさり解決します。
のグラフを追求していくと行き詰まります。文字定数は分離する(微分法の方程式への応用(2)を参照)、という定石であっさり解決します。
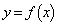 のグラフと
のグラフと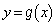 のグラフの共有点のx座標は、方程式
のグラフの共有点のx座標は、方程式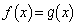 の解です。
の解です。
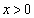 なので、両辺をxで割ると、
なので、両辺をxで割ると、
この解は、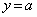 と
と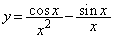 を連立したときの解です。
を連立したときの解です。
とおくと、
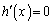 とすると、
とすると、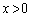 においては、
においては、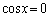 より
より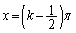 (
(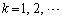 )
)
xが0に近いところでの増減表は以下のようになります(関数の増減を参照)。
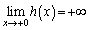 であり、
であり、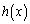 の極値について、
の極値について、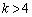 の場合は、
の場合は、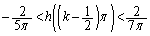 となるので、増減表より、
となるので、増減表より、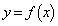 のグラフと
のグラフと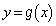 のグラフが
のグラフが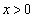 において共有点をちょうど3つ持つaは、
において共有点をちょうど3つ持つaは、
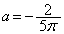 ,
,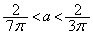 .......[答]
.......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。