東京大学理系2013年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 実数a,bに対し平面上の点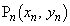 を
を
によって定める。このとき、次の条件(i),(ii)がともに成り立つような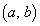 をすべて求めよ。
をすべて求めよ。
(i) 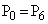
[解答へ]
[2] aを実数とし、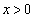 で定義された関数
で定義された関数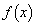 ,
,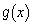 を次のように定める。
を次のように定める。
このとき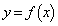 のグラフと
のグラフと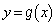 のグラフが
のグラフが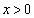 において共有点をちょうど3つ持つようなaをすべて求めよ。
において共有点をちょうど3つ持つようなaをすべて求めよ。
[解答へ]
[3] A,Bの2人がいる。投げたとき表裏の出る確率がそれぞれ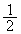 のコインが1枚あり、最初はAがそのコインを持っている。次の操作を繰り返す。
のコインが1枚あり、最初はAがそのコインを持っている。次の操作を繰り返す。
(i) Aがコインを持っているときは、コインを投げ、表が出ればAに1点を与え、コインはAがそのまま持つ。裏が出れば、両者に点を与えず、AはコインをBに渡す。
(ii) Bがコインを持っているときは、コインを投げ、表が出ればBに1点を与え、コインはBがそのまま持つ。裏が出れば、両者に点を与えず、BはコインをAに渡す。
そしてA,Bのいずれかが2点を獲得した時点で、2点を獲得した方の勝利とする。たとえば、コインが表、裏、表、表と出た場合、この時点でAは1点、Bは2点を獲得しているのでBの勝利となる。
(1) A,Bあわせてちょうどn回コインを投げ終えたときにAの勝利となる確率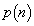 を求めよ。
を求めよ。 (2) 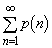 を求めよ。
を求めよ。 [解答へ]
[4] △ABCにおいて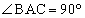 ,
,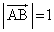 ,
,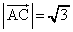 とする。△ABCの内部の点Pが
とする。△ABCの内部の点Pが
を満たすとする。
(1) 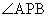 ,
,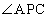 を求めよ。
を求めよ。 [解答へ]
[5] 次の命題を証明したい。
命題P 次の条件(a),(b)をともに満たす自然数(1以上の整数)Aが存在する。
(a) Aは連続する3つの自然数の積である。
(b) Aを10進法で表したとき、1が連続して99回以上現れるところがある。
以下の問いに答えよ。
(1) yを自然数とする。このとき不等式
が成り立つような正の実数xの範囲を求めよ。
(2) 命題Pを証明せよ。
[解答へ]
[6] 座標空間において、xy平面内で不等式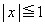 ,
,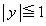 により定まる正方形Sの4つの頂点をA
により定まる正方形Sの4つの頂点をA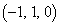 ,B
,B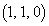 ,C
,C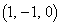 ,D
,D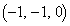 とする。正方形Sを、直線BDを軸として回転させてできる立体を
とする。正方形Sを、直線BDを軸として回転させてできる立体を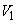 ,直線ACを軸として回転させてできる立体を
,直線ACを軸として回転させてできる立体を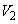 とする。
とする。
(1) 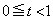 を満たす実数t に対し、平面
を満たす実数t に対し、平面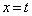 による
による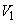 の切り口の面積を求めよ。
の切り口の面積を求めよ。 (2) 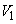 と
と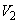 の共通部分の体積を求めよ。
の共通部分の体積を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。