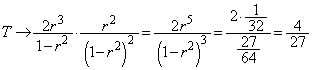���嗝�n���w'13�N�O��[3]
A�CB��2�l������B�������Ƃ��\���̏o��m�������ꂼ��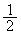 �̃R�C����1������A�ŏ���A�����̃R�C���������Ă���B���̑�����J��Ԃ��B
�̃R�C����1������A�ŏ���A�����̃R�C���������Ă���B���̑�����J��Ԃ��B
(i) A���R�C���������Ă���Ƃ��́A�R�C���𓊂��A�\���o���A��1�_��^���A�R�C����A�����̂܂��B�����o��A���҂ɓ_��^�����AA�̓R�C����B�ɓn���B
(ii) B���R�C���������Ă���Ƃ��́A�R�C���𓊂��A�\���o���B��1�_��^���A�R�C����B�����̂܂��B�����o��A���҂ɓ_��^�����AB�̓R�C����A�ɓn���B
������A�CB�̂����ꂩ��2�_���l���������_�ŁA2�_���l���������̏����Ƃ���B���Ƃ��A�R�C�����\�A���A�\�A�\�Əo���ꍇ�A���̎��_��A��1�_�AB��2�_���l�����Ă���̂�B�̏����ƂȂ�B
(1) A�CB���킹�Ă��傤��n��R�C���𓊂��I�����Ƃ���A�̏����ƂȂ�m��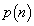 �����߂�B
�����߂�B (2) 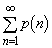 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����݂ɂ����̂ŁA�ŏ��́A�R�C����1���A2���A�Ƃ��Ă����Ƃǂ��Ȃ邩�A�Ă��˂��ɒ��ׂ܂��傤�B(2)�̋����a�̌v�Z�͂��܂�ɖʓ|�ŁA����I�ɂ͔�����̂�����ł��B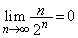 �C
�C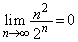 ���q���g�ɂȂ��Ă��Ȃ��̂ŁA�o��҂��ł���Ǝv���Ă��Ȃ��̂ł͂Ȃ����A�Ƃ����C�����܂��B
���q���g�ɂȂ��Ă��Ȃ��̂ŁA�o��҂��ł���Ǝv���Ă��Ȃ��̂ł͂Ȃ����A�Ƃ����C�����܂��B
(1) �R�C����1����A�������Ƃ͂Ȃ��̂ŁA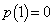 �ł��B
�ł��B �R�C����2����A����������̂́A�\�\�A�Əo���ꍇ�ŁA�����m����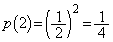 �ł��B
�ł��B
�R�C����3����A�������Ƃ͂Ȃ��̂ŁA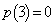 �ł��B
�ł��B
�R�C����4����A�����̂́A�\�����\�A�Əo�邩�A�����\�\�A�Əo��ꍇ�ŁA���̊m���́A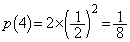 �ł��B
�ł��B
�R�C����5����A�����̂́A�\���\���\�A�Əo�邩�A���\���\�\�A�Əo��ꍇ�ŁA���̊m���́A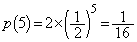 �ł��B
�ł��B
���̂Ƃ��́AB��1�_�l�����Ă��邱�Ƃɒ��ӂ��Ă��������B
�R�C����6����A�����̂́A�\���������\�A�Əo�邩�A�����\�����\�A�Əo�邩�A���������\�\�A�Əo��ꍇ�ŁA���̊m���́A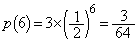 �ł��B
�ł��B
���̂Ƃ��́AB��0�_�ł��B
����ŁA�R�C������������Ƃ��Ɗ����Ƃ��ƂňႢ�����肻�����A�Ƃ������Ƃ��킩��܂��B
�R�C����7����A�����̂́A�\���\�������\�A�\�������\���\�A���\���\�����\�A���\�������\�\�A�����\���\���\�A�������\���\�\�A�Əo��ꍇ�ŁA���̊m���́A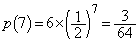 �ł��B
�ł��B
���̂Ƃ��́AB��1�_�l�����Ă��܂��B�܂��A���͑S����4��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A�܂��́A2��A�܂��́A4��o����ɕ\���o��ꍇ�ŁA3�ʂ肠��܂��BB��1�_�^������̂́A����1��A�܂��́A3��o����ɕ\���o��ꍇ�ŁA2�ʂ肠��܂��B
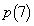 ��
��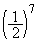 ��6��������̂́A�\���̃p�^�[����
��6��������̂́A�\���̃p�^�[����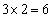 �ʂ肠�邩��ł��B
�ʂ肠�邩��ł��B
�R�C����8���āAA�����̂́A�\�������������\�A�����\���������\�A���������\�����\�A�������������\�\�A�Əo��ꍇ�ŁA���̊m���́A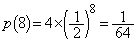 �ł��B
�ł��B
���̂Ƃ��́AB��0�_�ł��B���͑S����6��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A2��A4��A6��o����ɕ\���o��ꍇ�ŁA4�ʂ肠��܂��B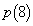 ��
��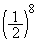 ��4��������̂́A�\���̃p�^�[����4�ʂ肠�邩��ł��BA���ŏI�I�ɏ����߂ɂ́A����������o�Ă��čŌ�ɕ\���o��K�v������܂����AB�̔Ԃ̂Ƃ��ɕ\���o��B��1�_�^�����Ă���ƁAA�̍Ō�̔Ԃ������Ƃ��ɁA
��4��������̂́A�\���̃p�^�[����4�ʂ肠�邩��ł��BA���ŏI�I�ɏ����߂ɂ́A����������o�Ă��čŌ�ɕ\���o��K�v������܂����AB�̔Ԃ̂Ƃ��ɕ\���o��B��1�_�^�����Ă���ƁAA�̍Ō�̔Ԃ������Ƃ��ɁA (i) A��0�_�Ȃ�A������̗���1��̕\���o�Ă���A�����܂łɃR�C���͊�����Ă��āA��������\��2��o��A�����ƁA�R�C�������̉͊�ł��B
(ii) A��1�_�Ȃ�A������̗���2��̕\���o�Ă���A�����܂łɃR�C���͋��������Ă��āA��������\��1��o��A�����ƁA�R�C�������̉͊�ł��B
������ɂ��Ă��AB��1�_�l�����Ă���A�����̂́A�R�C�������̉���̂Ƃ��ł��B
�R�C�������̉�������A�����Ƃ��ɂ�B�̓��_��0�C�R�C�������̉����A�����Ƃ��ɂ́AB�̓��_��1�ł��B
�]���āA�R�C����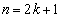 ��(
��(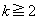 )������A�����Ƃ��AB�̓��_��1�ŁA�\��3��o��̂ŁA����
)������A�����Ƃ��AB�̓��_��1�ŁA�\��3��o��̂ŁA����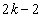 ��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A2��A����A
��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A2��A����A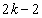 ��o����ɕ\���o��ꍇ�ŁAk�ʂ肠��܂��BB��1�_�^������̂́A����1��A3��A�����A
��o����ɕ\���o��ꍇ�ŁAk�ʂ肠��܂��BB��1�_�^������̂́A����1��A3��A�����A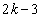 ��o����ɕ\���o��ꍇ�ŁA
��o����ɕ\���o��ꍇ�ŁA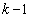 �ʂ肠��܂��B
�ʂ肠��܂��B
����āA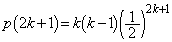 �@(
�@(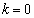 �C
�C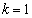 �̂Ƃ������藧���܂�)�R�C����
�̂Ƃ������藧���܂�)�R�C����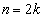 ����(
����(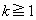 )A�����Ƃ��AB�̓��_��0�ŁA�\��2��o��̂ŁA����
)A�����Ƃ��AB�̓��_��0�ŁA�\��2��o��̂ŁA����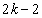 ��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A2��A����A
��o�܂��BA�ɍŏ���1�_���^������̂́A����0��A2��A����A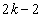 ��o����ɕ\���o��ꍇ�ŁAk�ʂ肠��܂��B
��o����ɕ\���o��ꍇ�ŁAk�ʂ肠��܂��B
����āA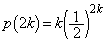
�ȏ���An����̂Ƃ��A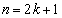 �C
�C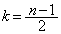 ���A
���A n�������̂Ƃ��A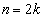 �C
�C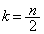 ���A
���A 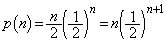 ......[��]
......[��]
(2) n�̋��ŕ����Ęa�����߂܂�(�����������Q��)�B�ȉ��ŁA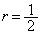 �Ƃ��܂��B
�Ƃ��܂��B �Ƃ���ƁA
�� 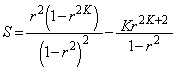 �@����@
�@����@
�����ŁA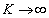 �Ƃ���ƁA
�Ƃ���ƁA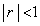 ���
���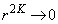 �C
�C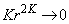 ���A
���A 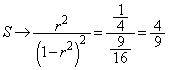 �@����A
�@����A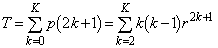
�Ƃ���ƁA
����āA����ƇB�Ƃ���A
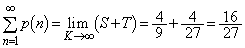 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 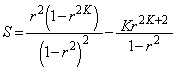 �@����@
�@����@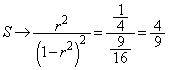 �@����A
�@����A