���嗝�n���w'13�N�O��[6]
���W��Ԃɂ����āAxy���ʓ��ŕs����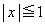 �C
�C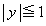 �ɂ���܂鐳���`S��4�̒��_��A
�ɂ���܂鐳���`S��4�̒��_��A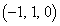 �CB
�CB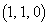 �CC
�CC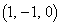 �CD
�CD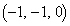 �Ƃ���B�����`S���A����BD�����Ƃ��ĉ�]�����Ăł��闧�̂�
�Ƃ���B�����`S���A����BD�����Ƃ��ĉ�]�����Ăł��闧�̂�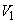 �C����AC�����Ƃ��ĉ�]�����Ăł��闧�̂�
�C����AC�����Ƃ��ĉ�]�����Ăł��闧�̂�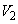 �Ƃ���B
�Ƃ���B
(1) 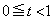 ��������t �ɑ��A����
��������t �ɑ��A����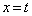 �ɂ��
�ɂ��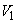 �̐���̖ʐς����߂�B
�̐���̖ʐς����߂�B (2) 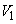 ��
��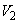 �̋��ʕ����̑̐ς����߂�B
�̋��ʕ����̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��̂悤�ɍׂ����������Ă���ƁA�ƂĂ��Ō�܂ł��ǂ���܂���B���m�Ș_�q�͓���ł��A���ϖ��Ƃ��Ă͕K������������ł͂���܂���B�~�������ɕ��s�ȕ��ʂŐ�Ɛ���͕������ł��B����I�ɂ́A�Ώ̐������o�I�Ɍ��j���Čv�Z��i�߁A�������ł��o���Ă����悤�ɂ��܂��傤�B
(1) �����`S��xy���ʓ��ŁA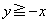 �Ɉʒu���镔���ƁA
�Ɉʒu���镔���ƁA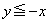 �Ɉʒu���镔���ɕ�����
�Ɉʒu���镔���ɕ�����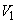 ���l���܂��B
���l���܂��B (i) �܂��A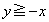 �Ɉʒu���镔���ɂ��āA
�Ɉʒu���镔���ɂ��āA ��BC��̓_��y���W��u (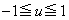 )�Ƃ��āAP
)�Ƃ��āAP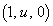 ��ʂ�xy�ʏ�Œ���BD�ɐ����Ȓ����́A
��ʂ�xy�ʏ�Œ���BD�ɐ����Ȓ����́A ����ƒ���BD�F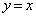 �Ƃ̌�_�́A
�Ƃ̌�_�́A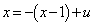 ���A
���A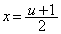 P���AQ
P���AQ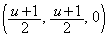 �𒆐S�Ƃ��Ē���BD�ɐ����ȕ���(xy���ʂƂ̌���͇@)���ʼn�]������ƁA
�𒆐S�Ƃ��Ē���BD�ɐ����ȕ���(xy���ʂƂ̌���͇@)���ʼn�]������ƁA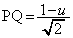 ���A
���A 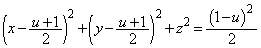 (��ԍ��W���Q��) ����
(��ԍ��W���Q��) ���� 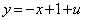
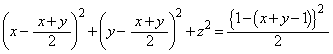 �@(u������)
�@(u������)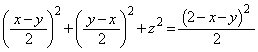
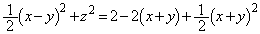
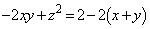
����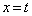 (
(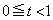 )�Ő�ƁA
)�Ő�ƁA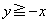 �Ɉʒu���镔�����l���Ă���̂�
�Ɉʒu���镔�����l���Ă���̂�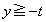 �ł����āA����́A
�ł����āA����́A �� 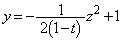 �@(
�@(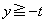 )�@����A
)�@����A (ii) 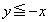 �Ɉʒu���镔���ɂ��āA
�Ɉʒu���镔���ɂ��āA ��AD��̓_��y���W��u (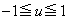 )�Ƃ��āAP
)�Ƃ��āAP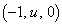 ��ʂ�xy���ʏ�Œ���BD�ɐ����Ȓ����́A
��ʂ�xy���ʏ�Œ���BD�ɐ����Ȓ����́A 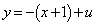 �@����B
�@����B����ƒ���BD�F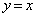 �Ƃ̌�_�́A
�Ƃ̌�_�́A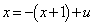 ���A
���A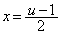 P���AQ
P���AQ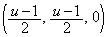 �𒆐S�Ƃ��Ē���BD�ɐ����ȕ���(xy���ʂƂ̌���͇B)���ʼn�]������ƁA
�𒆐S�Ƃ��Ē���BD�ɐ����ȕ���(xy���ʂƂ̌���͇B)���ʼn�]������ƁA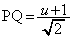 ���A
���A ����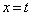 (
(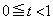 )�Ő�ƁA
)�Ő�ƁA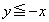 �Ɉʒu���镔�����l���Ă���̂ŁA
�Ɉʒu���镔�����l���Ă���̂ŁA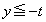 �ł����āA����́A
�ł����āA����́A �� 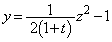 �@(
�@(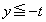 )�@����C
)�@����C ����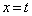 �ɂ��
�ɂ��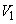 �̐���́A(����
�̐���́A(����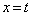 ���)�B�ƇC�Ɉ͂܂ꂽ�}�`�ɂȂ�܂��B
���)�B�ƇC�Ɉ͂܂ꂽ�}�`�ɂȂ�܂��B
�B��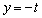 ��A������ƁA
��A������ƁA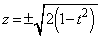
�C��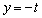 ��A������ƁA
��A������ƁA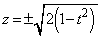
����āA����̖ʐς́A 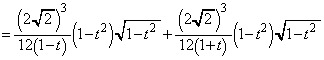
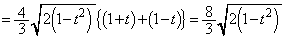 ......[��]
......[��]���D�v����ɁA������������Ƃ킩���Ă��āA�ϕ�����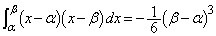 �̗��p���l����̂ł���A����
�̗��p���l����̂ł���A����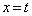 �Ő����Ƃ��̕������̊J����ƁA��������
�Ő����Ƃ��̕������̊J����ƁA��������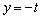 �Ƃ�2��_�̋���
�Ƃ�2��_�̋���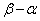 ���킩��悢�킯�ł��B
���킩��悢�킯�ł��B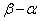 �́A�~
�́A�~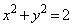 ������
������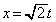 ����錷�̒����Ƃ���
����錷�̒����Ƃ���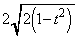 (�~�ƒ����̈ʒu�W���Q��)�C�J����́A�������̎���
(�~�ƒ����̈ʒu�W���Q��)�C�J����́A�������̎���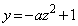 �Ƃ����A
�Ƃ����A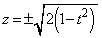 �̂Ƃ�
�̂Ƃ�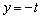 �Ƃ���
�Ƃ���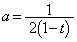 �ȂǂƂ���ΊȒP�ɋ��߂��܂�(2�������Q��)�B
�ȂǂƂ���ΊȒP�ɋ��߂��܂�(2�������Q��)�B
(2) 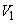 ��
��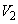 �Ƃʼn����Ⴄ���A�Ƃ������Ƃ��l���Ă݂܂��B
�Ƃʼn����Ⴄ���A�Ƃ������Ƃ��l���Ă݂܂��B xy���ʏ�ɂ����āA�����`S�Ɖ�]��BD�̑g�ݍ��킹�́A�����`S�Ɖ�]��AC�̑g�ݍ��킹�ƁAy���Ɋւ��Đ��Ώ̂ł��B��]�̂������������Ȃ̂ŁA��]��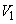 ��
��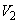 �Ƃ͕���
�Ƃ͕���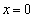 ����yz���ʂɊւ��đΏ̂ł��B(1)�ł́A
����yz���ʂɊւ��đΏ̂ł��B(1)�ł́A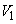 ���Ax����
���Ax����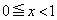 �̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐�����l���܂����B���̕�����
�̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐�����l���܂����B���̕�����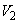 �Ƃ̋��ʕ������l����̂ł���A�Ώ̐�����A
�Ƃ̋��ʕ������l����̂ł���A�Ώ̐�����A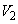 ���Ax����
���Ax����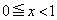 �̕�����ʉ߂���x���ɐ����ȕ��ʂŐ���������l�������ɁA
�̕�����ʉ߂���x���ɐ����ȕ��ʂŐ���������l�������ɁA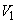 ���Ax����
���Ax����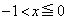 �̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐�����l����悢���ƂɂȂ�܂��B
�̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐�����l����悢���ƂɂȂ�܂��B
�܂��Axy���ʏ�ɂ����āA�����`S�Ɖ�]��BD�̑g�ݍ��킹��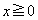 �̕�����
�̕�����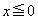 �̕����Ƃ́A���_O�Ɋւ��ē_�Ώ̂ł��B
�̕����Ƃ́A���_O�Ɋւ��ē_�Ώ̂ł��B ���Ax����
���Ax����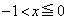 �̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐���́A
�̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐���́A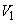 ���Ax����
���Ax����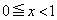 �̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐����z���̉���
�̕�����ʉ߂���x���Ɛ����ȕ��ʂŐ����Ƃ��̐����z���̉���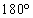 ��]���������̂ɂȂ�܂��B
��]���������̂ɂȂ�܂��B
�]���āA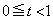 �Ƃ��āA����
�Ƃ��āA����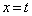 �ɂ��
�ɂ��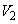 �̐���́A����
�̐���́A����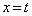 ��ɂ����āA�A�C�C��y���Ɋւ��đΏ̂ȁA
��ɂ����āA�A�C�C��y���Ɋւ��đΏ̂ȁA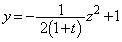 ��
��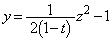 �ɋ��܂ꂽ�}�`�ɂȂ�܂��B
�ɋ��܂ꂽ�}�`�ɂȂ�܂��B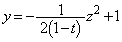 ��
��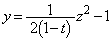 �Ƃ́A
�Ƃ́A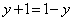 ���
���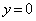 �C
�C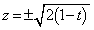 �C�܂�A
�C�܂�A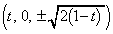 �ɂ����Č����܂��B
�ɂ����Č����܂��B �ɂ����ẮA
�ɂ����ẮA �ƂȂ�̂ŁA �C
�C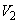 �̋��ʕ�����
�̋��ʕ�����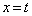 �Ő�������́A
�Ő�������́A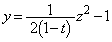 ��
��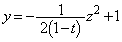 �ɋ��܂ꂽ�}�`�ɂȂ�܂��B
�ɋ��܂ꂽ�}�`�ɂȂ�܂��B
���̖ʐ�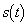 �́A
�́A ���߂�̐ς́A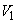 ��yz���ʂɊւ���
��yz���ʂɊւ���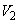 �ƑΏ̂Ȃ��Ƃ���A
�ƑΏ̂Ȃ��Ƃ���A 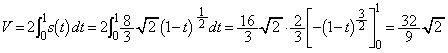 ......[��]
......[��]���D���ĂƂ��ẮA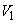 ��yz���ʂɊւ���
��yz���ʂɊւ���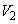 �ƑΏ̂ŁA
�ƑΏ̂ŁA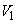 ��z���Ɋւ���
��z���Ɋւ���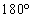 ��]����Ǝ��g�ɏd�Ȃ邱�Ƃ�f��A���Ƃ͌v�Z�ߒ����������x�őË����ׂ��ł��B
��]����Ǝ��g�ɏd�Ȃ邱�Ƃ�f��A���Ƃ͌v�Z�ߒ����������x�őË����ׂ��ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 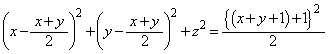 �@(u������)
�@(u������)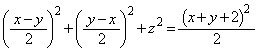
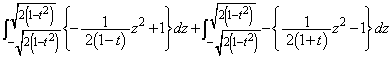
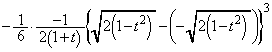
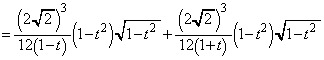
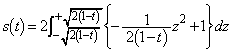
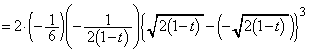
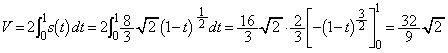 ......[��]
......[��]