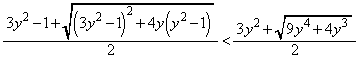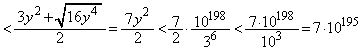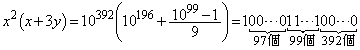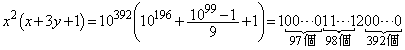���嗝�n���w'13�N�O��[5]
���̖�����ؖ��������B
����P�@���̏���(a)�C(b)���Ƃ��ɖ��������R��(1�ȏ�̐���)A�����݂���B
(a) A�͘A������3�̎��R���̐ςł���B
(b) A��10�i�@�ŕ\�����Ƃ��A1���A������99��ȏ㌻���Ƃ��낪����B
�ȉ��̖₢�ɓ�����B
(1) y�����R���Ƃ���B���̂Ƃ��s����
�����藧�悤�Ȑ��̎���x�͈̔͂����߂�B
(2) ����P���ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͌������͋X�����ł����A���}�ł��B(2)�́A�S�^���Ă���(1)�̕s�������ǂ��g���̂��A�Ƃ������ƂɔY�܂���܂��B
(1) ���ӂ�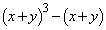 �ƕό`�ł���̂ŁA�ؖ����ׂ��s�����̊e�ӂ���
�ƕό`�ł���̂ŁA�ؖ����ׂ��s�����̊e�ӂ���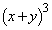 ���������Ƃɂ��A
���������Ƃɂ��A �@�̉E���̕s�����́A���R��y�ɂ��āA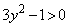 �C
�C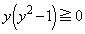 ���A
���A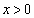 �ɂ����āA
�ɂ����āA 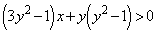 �@����A
�@����A���A�˂ɐ��藧���܂��B
�@�̍����̕s�������A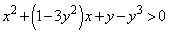
�Ƃ����ƁA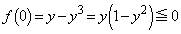 ���Ax��2��������
���Ax��2��������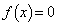 ��
��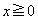 �ƂȂ���������܂��B
�ƂȂ���������܂��B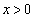 �͈̔͂�
�͈̔͂�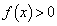 �ƂȂ�����́Ax���A
�ƂȂ�����́Ax���A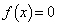 ��
��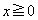 �ƂȂ�������傫���Ȃ邱�Ƃł��B�@(2���������̈�ʘ_���Q��)����āA�A�ƍ��킹�āA���߂�x�͈̔͂́A
�ƂȂ�������傫���Ȃ邱�Ƃł��B�@(2���������̈�ʘ_���Q��)����āA�A�ƍ��킹�āA���߂�x�͈̔͂́A 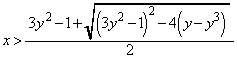 �@����B
�@����B�� 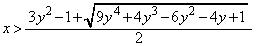 ......[��]
......[��]
(2) (1)�̕s���������������āA
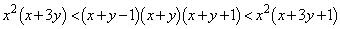 �@����C
�@����C���ӂ́Ax�������Ƃ���A�A��3�����̐ςɂȂ��Ă���̂ŁA�����A�ƍl����AA�́A1���A������99��ȏ㌻���Ƃ��낪����2�̐��̊Ԃɋ��܂��͂��ł��B�܂�A���ӂ�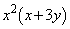 �ƉE�ӂ�
�ƉE�ӂ�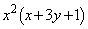 �́A�Ƃ���1���A������99��ȏ㌻��鐔�ɂȂ�͂��ł��B
�́A�Ƃ���1���A������99��ȏ㌻��鐔�ɂȂ�͂��ł��B
�Ƃ���ŁA�u1���A������99��ȏ㌻��鐔�v�Ŏv���o���̂́A���嗝�n08�N[5]�ł��B1��n�A�����ĕ��Ԑ����́A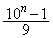 �ƕ\����܂��B1��99�A�����ĕ��Ԑ����́A
�ƕ\����܂��B1��99�A�����ĕ��Ԑ����́A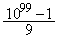 �ƕ\����܂��B
�ƕ\����܂��B
�C�̕s�����𐬂藧�����邽�߂ɂ́A�B�����悤��x�����Ȃ�傫���Ƃ�Ηǂ��킯�ł����A1�̕��тɉe����^���Ȃ��悤�ɁAx��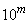 (m�͎��R��)�̌`�̑傫�Ȑ��ɂȂ�悤�ɂ���ƁA
(m�͎��R��)�̌`�̑傫�Ȑ��ɂȂ�悤�ɂ���ƁA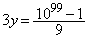 �Ƃ���Ηǂ������ł��B
�Ƃ���Ηǂ������ł��B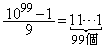 ��9�̔{���Ȃ̂ŁA
��9�̔{���Ȃ̂ŁA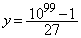 �͎��R���ł��B
�͎��R���ł��B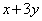 ��x���A
��x���A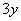 �̘A��99��1�ɉe����^���Ȃ��悤�ɂ���ɂ́A
�̘A��99��1�ɉe����^���Ȃ��悤�ɂ���ɂ́A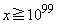 �Ƃ���悢�̂ł����A
�Ƃ���悢�̂ł����A
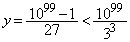 ���
���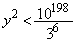
���A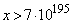 �ƂȂ�悤�ɁA�Ⴆ�A
�ƂȂ�悤�ɁA�Ⴆ�A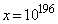 �C
�C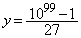 �Ƃ���A�B����������āA�s�����C�����藧���܂��B���̂Ƃ��A�s�����C�̍��ӂ́A
�Ƃ���A�B����������āA�s�����C�����藧���܂��B���̂Ƃ��A�s�����C�̍��ӂ́A �C�̉E�ӂ́A
����āA�s�����C�́A
x�Cy�Ƃ��Ɏ��R���Ȃ̂ŁA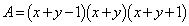 �����R���ŁA���̕s�������A�A��3���R���̐�A�ɂ́A1���A������99���Ƃ��낪����܂�(
�����R���ŁA���̕s�������A�A��3���R���̐�A�ɂ́A1���A������99���Ƃ��낪����܂�(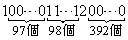 ���������������́A
���������������́A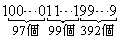 �ȉ��̐����ł�)�B����āA����P���������܂��B
�ȉ��̐����ł�)�B����āA����P���������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 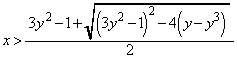 �@����B
�@����B