���嗝�n���w'19�N�O��[3]
���W��ԓ���5�_A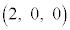 �CB
�CB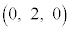 �CC
�CC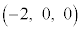 �CD
�CD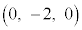 �CE
�CE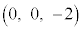 ���l����B����AB�̒��_M�Ɛ���AD�̒��_N��ʂ�A����AE�ɕ��s�ȕ��ʂ�α�Ƃ���B����ɁAp��
���l����B����AB�̒��_M�Ɛ���AD�̒��_N��ʂ�A����AE�ɕ��s�ȕ��ʂ�α�Ƃ���B����ɁAp��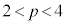 ���݂��������Ƃ��A�_P
���݂��������Ƃ��A�_P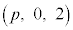 ���l����B
���l����B
(1) ���ʑ�PABCDE�̕���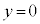 �ɂ��������сA����α�̕���
�ɂ��������сA����α�̕���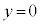 �ɂ�����ꕽ�ʏ�ɐ}������B
�ɂ�����ꕽ�ʏ�ɐ}������B (2) ���ʑ�PABCDE�̕���α�ɂ���������p�`�ƂȂ�p�͈̔͂����߂�B
(3) ����p��(2)�Œ�܂�͈͂ɂ���Ƃ���B���ʑ�PABCDE�̕���α�ɂ�����̓�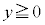 �C
�C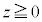 �̕�����_
�̕�����_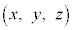 �������Ƃ��A���W���ʏ�œ_
�������Ƃ��A���W���ʏ�œ_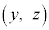 �������͈̖͂ʐς����߂�B
�������͈̖͂ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��Ԃ̂������Ԑ}�`�̖��ł����A���ʑ̂̊e�ӂƕ��ʂƂ̌�_���R�c�R�c���ׂĂ����A�ł��Ȃ����ł͂���܂���B
�܂��A����α�������������߂Ă����܂��B
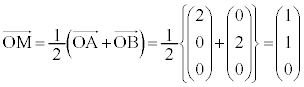 �@����@
�@����@
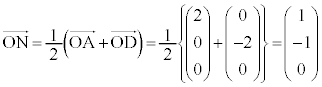
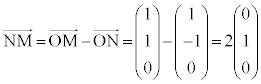 �@(
�@(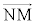 ��y���ɕ��s�ȃx�N�g���ł�)
��y���ɕ��s�ȃx�N�g���ł�)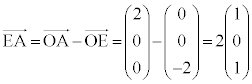
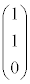 ��ʂ�A2�̃x�N�g��
��ʂ�A2�̃x�N�g��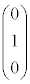 �C
�C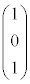 �ɂ���Ē����镽�ʂł����āAs�Ct�������Ƃ��āA����α��̓_F
�ɂ���Ē����镽�ʂł����āAs�Ct�������Ƃ��āA����α��̓_F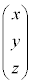 �́A
�́A
������A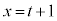 �C
�C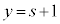 �C
�C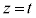 �C����α��̓_
�C����α��̓_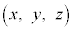 �ɂ��āA
�ɂ��āA
�@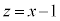 �@����A
�@����A
�Ƃ����W(�A�͕���α�̕������ł�)������܂��B
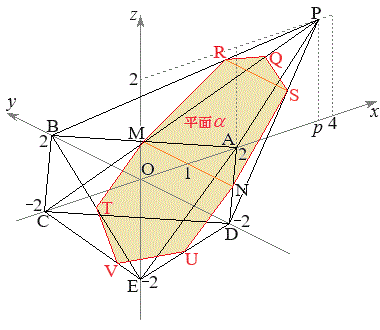
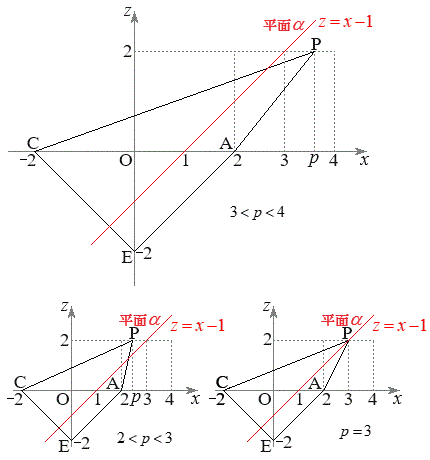 (1) ���ʑ�PABCDE�̒��_P�CA�CC�CE�́A����
(1) ���ʑ�PABCDE�̒��_P�CA�CC�CE�́A����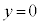 ��̓_�ł��B���ʑ̂�
��̓_�ł��B���ʑ̂�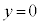 �Ő�ƁA����͎l�p�`PAEC (
�Ő�ƁA����͎l�p�`PAEC (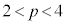 �Ȃ̂ŁAP�CE�CC���꒼����ɕ��Ԃ��Ƃ͂���܂���)�ł��B
�Ȃ̂ŁAP�CE�CC���꒼����ɕ��Ԃ��Ƃ͂���܂���)�ł��B����α�̕���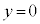 �ɂ�����́A�A���A����
�ɂ�����́A�A���A����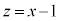 �ɂȂ�܂��B
�ɂȂ�܂��B
����āA�}������ƉE�}(�l�p�`PAEC�͍����A����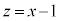 �͐Ԑ�)�B
�͐Ԑ�)�B ���D(1)�́A�ȍ~�̖����l�����ŁAy���ɕ��s�ȕ������璭�߂čl����悤�ɁA�Ƃ����U���ɂȂ��Ă��邾���Ȃ̂ŁAp�ɂ��ďꍇ�������ē�����K�v�͂Ȃ��Ǝv���܂����Ap�̒l�ɂ���ĕ���α�Ɣ��ʑ̂̈ʒu�W���ς��̂ŁA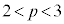 (��PA�ƕ���α����_�������A��PC�ƕ���α�͌�_�������Ȃ�)�C
(��PA�ƕ���α����_�������A��PC�ƕ���α�͌�_�������Ȃ�)�C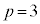 (�_P������α��)�C
(�_P������α��)�C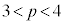 (��PC�ƕ���α����_�������A��PA�ƕ���α�͌�_�������Ȃ�)�ŁA�ꍇ�������ĉ���Ό����ł����A(2)�̐ݖ₪���Ӗ��ɂȂ�܂��B�@
(��PC�ƕ���α����_�������A��PA�ƕ���α�͌�_�������Ȃ�)�ŁA�ꍇ�������ĉ���Ό����ł����A(2)�̐ݖ₪���Ӗ��ɂȂ�܂��B�@
 (2) ���ʑ�PABCDE�̕���α�ɂ���������p�`�ƂȂ�̂́A�E�}�̂悤�ɂȂ�ꍇ�ł��B����α�Ɣ��ʑ�PABCDE�̕�PC�C��PB�C��PD�Ƃ���_Q�CR�CS�������A����α�Ɣ��ʑ�PABCDE�̕�AB�C��AD�Ƃ���_M�CN�������A����α�Ɣ��ʑ�PABCDE�̕�EB�C��ED�C��EC�Ƃ���_T�CU�CV�������A��������p�`QRMTVUNS�ɂȂ�܂��B����α�Ɣ��ʑ�PABCDE�̕�PA�C��BC�C��CD�C��EA�Ƃ͌�_�������܂���B
(2) ���ʑ�PABCDE�̕���α�ɂ���������p�`�ƂȂ�̂́A�E�}�̂悤�ɂȂ�ꍇ�ł��B����α�Ɣ��ʑ�PABCDE�̕�PC�C��PB�C��PD�Ƃ���_Q�CR�CS�������A����α�Ɣ��ʑ�PABCDE�̕�AB�C��AD�Ƃ���_M�CN�������A����α�Ɣ��ʑ�PABCDE�̕�EB�C��ED�C��EC�Ƃ���_T�CU�CV�������A��������p�`QRMTVUNS�ɂȂ�܂��B����α�Ɣ��ʑ�PABCDE�̕�PA�C��BC�C��CD�C��EA�Ƃ͌�_�������܂���B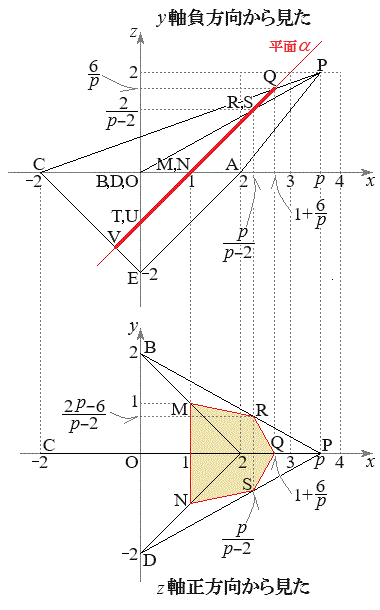 (3)
(3) 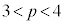 �̂Ƃ��̏��Ay�����������猩���ꍇ�ƁAz�����������猩���ꍇ�ɂ��āA�E�}�Ɏ����܂��B
�̂Ƃ��̏��Ay�����������猩���ꍇ�ƁAz�����������猩���ꍇ�ɂ��āA�E�}�Ɏ����܂��B
����α�ƕ�PC�̌�_Q�̍��W�����߂܂��B����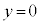 ��ŁA��PC�́A����
��ŁA��PC�́A����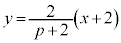 ��ɂ���܂��B����ƇA��A�������(2�����̌�_���Q��)�A
��ɂ���܂��B����ƇA��A�������(2�����̌�_���Q��)�A �� 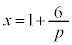 �C
�C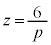 (�A���)�C����āAQ
(�A���)�C����āAQ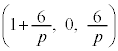 �@����B
�@����B
����α�ƕ�PB�̌�_R�̍��W�����߂܂��B�E��}�ŁA��PD�Ƃ̌�_S�ƁA��PB�Ƃ̌�_R�͏d�Ȃ��Č����܂��B�܂��A�_B�Ɠ_D�͓_O�ɏd�Ȃ��Č����܂��B��PB�ƕ�PD�͐���PO�ɏd�Ȃ��Č����܂��B�E��}�ŁA����PO�F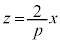 �ƇA��A������ƁA
�ƇA��A������ƁA �� 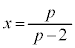 �C
�C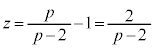
�E���}�ŁA�_P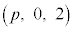 �͓_
�͓_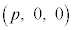 �ɏd�Ȃ��Č����܂��B�_R��y���W��y�Ƃ��ē_R�͓_
�ɏd�Ȃ��Č����܂��B�_R��y���W��y�Ƃ��ē_R�͓_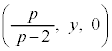 �ɏd�Ȃ��Č����܂��B����PB�́A����
�ɏd�Ȃ��Č����܂��B����PB�́A����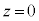 ���
���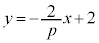 �ƂȂ�܂����A�����ŁA
�ƂȂ�܂����A�����ŁA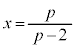 �Ƃ���ƁA
�Ƃ���ƁA ����āAR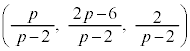 �@����C�@(�{��ɂ͖��W�ł����AS��R��y���W�̕������t�ɂȂ�܂�)
�@����C�@(�{��ɂ͖��W�ł����AS��R��y���W�̕������t�ɂȂ�܂�)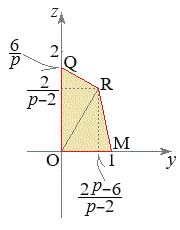 ���ʑ�PABCDE�̕���α�ɂ�����̂����A
���ʑ�PABCDE�̕���α�ɂ�����̂����A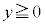 �C
�C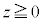 �̕�����_
�̕�����_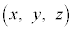 �������Ƃ��A���W���ʏ�œ_
�������Ƃ��A���W���ʏ�œ_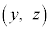 �������͈͂́A�E�}�̂悤�ɂȂ�܂��B�B�C�C�C�@���A�_Q�C�_R�C�_M�͕���
�������͈͂́A�E�}�̂悤�ɂȂ�܂��B�B�C�C�C�@���A�_Q�C�_R�C�_M�͕���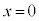 ��̓_
��̓_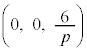 �C�_
�C�_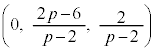 �C�_
�C�_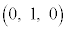 �ɏd�Ȃ��Č����܂��B
�ɏd�Ȃ��Č����܂��B
���߂�ʐς́A 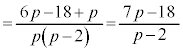 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 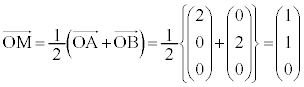 �@����@
�@����@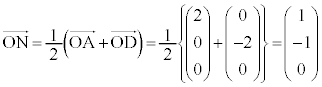
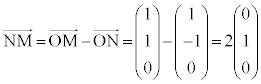 �@(
�@(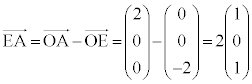
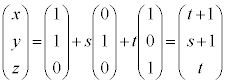
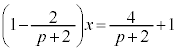
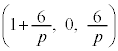 �@����B
�@����B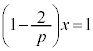
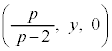 �ɏd�Ȃ��Č����܂��B����PB�́A����
�ɏd�Ȃ��Č����܂��B����PB�́A����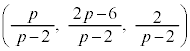 �@����C�@(�{��ɂ͖��W�ł����AS��R��y���W�̕������t�ɂȂ�܂�)
�@����C�@(�{��ɂ͖��W�ł����AS��R��y���W�̕������t�ɂȂ�܂�)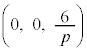 �C�_
�C�_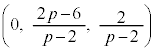 �C�_
�C�_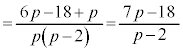 ......[��]
......[��]