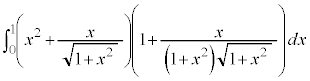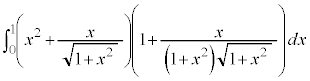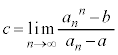東京大学理系2019年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の定積分を求めよ。
[解答へ]
[2] 一辺の長さが1の正方形ABCDを考える。3点P,Q,Rはそれぞれ辺AB,AD,CD上にあり、3点A,P,Qおよび3点P,Q,Rはどちらも面積が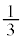 の三角形の3頂点であるとする。
の三角形の3頂点であるとする。
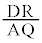 の最大値、最小値を求めよ。
の最大値、最小値を求めよ。
[解答へ]
[3] 座標空間の5点A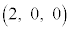 ,B
,B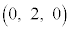 ,C
,C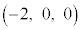 ,D
,D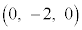 ,E
,E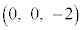 を考える。線分ABの中点Mと線分ADの中点Nを通り、直線AEに平行な平面をαとする。さらに、pは
を考える。線分ABの中点Mと線分ADの中点Nを通り、直線AEに平行な平面をαとする。さらに、pは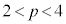 をみたす実数とし、点P
をみたす実数とし、点P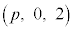 を考える。
を考える。
(1) 八面体PABCDEの平面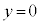 による切り口および、平面αの平面
による切り口および、平面αの平面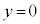 による切り口を同一平面上に図示せよ。
による切り口を同一平面上に図示せよ。 (2) 八面体PABCDEの平面αによる切り口が八角形となるpの範囲を求めよ。
(3) 実数pが(2)で定まる範囲にあるとする。八面体PABCDEの平面αによる切り口の内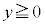 ,
,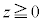 の部分を点
の部分を点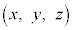 が動くとき、座標平面上で点
が動くとき、座標平面上で点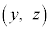 が動く範囲の面積を求めよ。
が動く範囲の面積を求めよ。 [解答へ]
[4] nを1以上の整数とする。
(2) 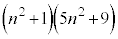 は整数の2乗にならないことを示せ。
は整数の2乗にならないことを示せ。 [解答へ]
[5] 以下の問いに答えよ。
(1) nを1以上の整数とする。xについての方程式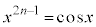 は、ただ一つの実数解
は、ただ一つの実数解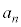 をもつことを示せ。
をもつことを示せ。 (2) (1)で定まる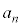 に対し、
に対し、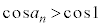 を示せ。
を示せ。 (3) (1)で定まる数列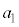 ,
,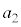 ,・・・・・・,
,・・・・・・,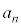 ,・・・・・・に対し、
,・・・・・・に対し、 を求めよ。
[解答へ]
[6] 複素数α,β,γ,δおよび実数a,bが、次の3条件をみたしながら動く。
条件1:α,β,γ,δは相異なる。
条件2:α,β,γ,δは4次方程式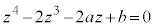 の解である。
の解である。 条件3:複素数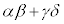 の実部は0であり、虚部は0でない。
の実部は0であり、虚部は0でない。 (1) α,β,γ,δのうち、ちょうど2つが実数であり、残りの2つは互いに共役な複素数であることを示せ。
(2) bをaで表せ。
(3) 複素数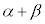 がとりうる範囲を複素数平面上に図示せよ。
がとりうる範囲を複素数平面上に図示せよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。