���嗝�n���w'19�N�O��[4]
n��1�ȏ�̐����Ƃ���B
(2) 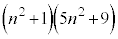 �͐�����2��ɂȂ�Ȃ����Ƃ������B
�͐�����2��ɂȂ�Ȃ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�́A�݂��ɑf�ł���2�̊�̐ς͕������łȂ��A�Ƃ͌����Ȃ��̂ŁA���ӂ��K�v�ł��B�Ⴆ�A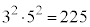 ��
��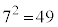 �݂͌��ɑf�ł����A���҂̐�
�݂͌��ɑf�ł����A���҂̐�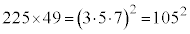 �͕������ł��B
�͕������ł��B
(1) 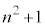 ��
��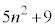 ���ő������m�Ƃ��܂��Bk�Cl�𐮐��Ƃ��āA
���ő������m�Ƃ��܂��Bk�Cl�𐮐��Ƃ��āA 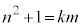 �@����@
�@����@
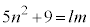 �@����A
�@����A�Ƃ����܂��B�A�|�@�~5���A
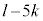 �͐����Ȃ̂ŁAm��4�̖ł���A
�͐����Ȃ̂ŁAm��4�̖ł���A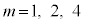 �Ɍ����܂��B���(��)
�Ɍ����܂��B���(��)�En����̂Ƃ�p�𐮐��Ƃ��āA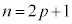 �Ƃ����ƁA
�Ƃ����ƁA ����āA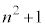 ��4�Ŋ����2�]�鐔�ŁA2�̔{���ł���4�̔{���ł͂���܂���B���̂Ƃ��A
��4�Ŋ����2�]�鐔�ŁA2�̔{���ł���4�̔{���ł͂���܂���B���̂Ƃ��A ����āA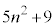 ��4�Ŋ����2�]�鐔�ŁA2�̔{���ł���4�̔{���ł͂���܂���B
��4�Ŋ����2�]�鐔�ŁA2�̔{���ł���4�̔{���ł͂���܂���B
�]���āA(��)���A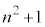 ��
��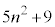 �̍ő����
�̍ő����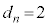 �ł��B
�ł��B �En�������̂Ƃ�p�𐮐��Ƃ��āA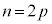 �Ƃ����ƁA
�Ƃ����ƁA �͊�ł��B
�͊�ł��B(��)���A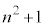 ��
��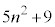 ��1�ȊO�̊�̖��������Ȃ��̂ŁA�ő����
��1�ȊO�̊�̖��������Ȃ��̂ŁA�ő����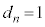 �ł��B
�ł��B �ȏ���An����̂Ƃ�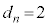 �Cn�������̂Ƃ�
�Cn�������̂Ƃ�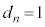 ......[��]
......[��]
(2) 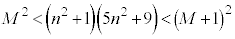 �ƂȂ鐮��M��T���A�Ƃ������j���l�����܂����A
�ƂȂ鐮��M��T���A�Ƃ������j���l�����܂����A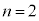 �̂Ƃ��A
�̂Ƃ��A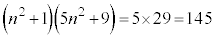 �ł����A
�ł����A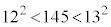 �Ƃ���Ƃ��́A
�Ƃ���Ƃ��́A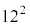 ��145�̍����������A�ȒP�ɍs������������܂���B���ۂɂ���Ă݂�ƁAM�̎����ɋK�������Ȃ��s���l��܂��B
��145�̍����������A�ȒP�ɍs������������܂���B���ۂɂ���Ă݂�ƁAM�̎����ɋK�������Ȃ��s���l��܂��B �����ŁA(1)�̗��p���l���邱�ƂɂȂ�܂��B
�En�������̂Ƃ��A(1)���A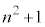 �C
�C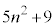 �݂͌��ɑf�Ȃ̂ŁA
�݂͌��ɑf�Ȃ̂ŁA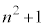 ��f�������������Ƃ��ɑf��p���܂ނƁA
��f�������������Ƃ��ɑf��p���܂ނƁA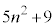 ��f�������������Ƃ��ɑf��p���܂݂܂���B
��f�������������Ƃ��ɑf��p���܂݂܂���B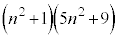 ���������ɂȂ邽�߂ɂ́A
���������ɂȂ邽�߂ɂ́A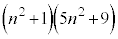 ��f�������������Ƃ��ɑf��p�������܂܂Ȃ���Ȃ�Ȃ��̂ŁA��������
��f�������������Ƃ��ɑf��p�������܂܂Ȃ���Ȃ�Ȃ��̂ŁA��������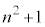 ��f�������������Ƃ��ɑf��p�������܂ނ��ƂɂȂ�܂��B�܂�
��f�������������Ƃ��ɑf��p�������܂ނ��ƂɂȂ�܂��B�܂�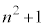 �͕������ł���K�v������܂��Bq�������̂Ƃ��A
�͕������ł���K�v������܂��Bq�������̂Ƃ��A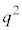 �C
�C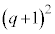 �͕������ł����A���̍��́A
�͕������ł����A���̍��́A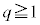 �̂Ƃ��A
�̂Ƃ��A �ł����āA������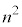 �ɑ��āA
�ɑ��āA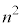 �Ƃ̍���1�ł���
�Ƃ̍���1�ł���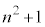 �͕������ɂȂ蓾�܂���B
�͕������ɂȂ蓾�܂���B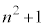 ���������ɂȂ蓾�Ȃ��̂ŁA
���������ɂȂ蓾�Ȃ��̂ŁA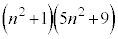 �͕������ɂȂ�܂���B
�͕������ɂȂ�܂���B �En����̂Ƃ��A(1)���A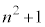 �C
�C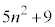 �͍ő����2�������܂��B
�͍ő����2�������܂��B p ��0�ȏ�̐����Ƃ��āA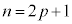 �Ƃ����ƁA
�Ƃ����ƁA 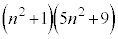 ��4�̔{���ł����An�������̂Ƃ��Ɠ��l�ɁA
��4�̔{���ł����An�������̂Ƃ��Ɠ��l�ɁA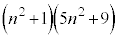 ���������ł��邽�߂ɂ́A
���������ł��邽�߂ɂ́A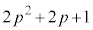 ��
��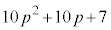 ���Ƃ��ɕ������łȂ���Ȃ�܂���Bs�Ct�𐮐��Ƃ��āA
���Ƃ��ɕ������łȂ���Ȃ�܂���Bs�Ct�𐮐��Ƃ��āA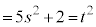 �@����@
�@����@�Ƃ����܂��B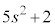 ��5�Ŋ����2�]�鐔�ł��Bm�𐮐��Ar��
��5�Ŋ����2�]�鐔�ł��Bm�𐮐��Ar��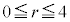 ���������Ƃ��āA
���������Ƃ��āA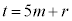 �Ƃ���(��]�����Q��)�ƁA
�Ƃ���(��]�����Q��)�ƁA 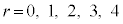 �̂Ƃ�
�̂Ƃ�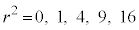 �C���̊e�X�ɑ��āA
�C���̊e�X�ɑ��āA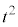 ��5�Ŋ������]��́A0�C1�C4�C4�C1�ł��B
��5�Ŋ������]��́A0�C1�C4�C4�C1�ł��B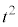 ��5�Ŋ������Ƃ��ɗ]��2�ɂȂ邱�Ƃ͂���܂���B����āA�����@���������邱�Ƃ͂���܂���B
��5�Ŋ������Ƃ��ɗ]��2�ɂȂ邱�Ƃ͂���܂���B����āA�����@���������邱�Ƃ͂���܂���B
�]����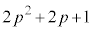 ��
��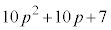 ���Ƃ��ɕ������ɂȂ邱�Ƃ͂Ȃ��A
���Ƃ��ɕ������ɂȂ邱�Ƃ͂Ȃ��A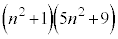 �͕������ɂȂ�܂���B
�͕������ɂȂ�܂���B�ȏ���A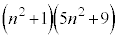 ��������2��ɂȂ�Ȃ����Ƃ�������܂����B
��������2��ɂȂ�Ȃ����Ƃ�������܂����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B