���嗝�n���w'19�N�O��[6]
���f��α�Cβ�Cγ�Cδ����ю���a�Cb���A����3�������݂����Ȃ��瓮���B
����1�Fα�Cβ�Cγ�Cδ�͑��قȂ�B
����2�Fα�Cβ�Cγ�Cδ��4��������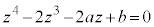 �̉��ł���B
�̉��ł���B ����3�F���f��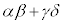 �̎�����0�ł���A������0�łȂ��B
�̎�����0�ł���A������0�łȂ��B (1) α�Cβ�Cγ�Cδ�̂����A���傤��2�������ł���A�c���2�݂͌��ɋ����ȕ��f���ł��邱�Ƃ������B
(2) b��a�ŕ\���B
(3) ���f��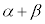 ���Ƃ肤��͈͂f�����ʏ�ɐ}������B
���Ƃ肤��͈͂f�����ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@4�����̃O���t���l�@���悤�Ƃ��Ă��Aa�Cb��2�����������Ă��ē���̂ŁA�����W����4���������ł́Az�����Ȃ�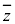 �����ɂȂ�(�������������Q��)�Ƃ����������g���čl�@��i�߂܂��B���q�ɂȂ��Ă��܂�������(2)�̒_(����)�́A(1)���
�����ɂȂ�(�������������Q��)�Ƃ����������g���čl�@��i�߂܂��B���q�ɂȂ��Ă��܂�������(2)�̒_(����)�́A(1)���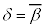 �Ƃ��āA
�Ƃ��āA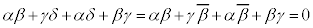 �ɋC�Â����ƂȂ̂ł���(�ȉ��ŇE���Ƃ���)�A���ꂪ�A�Ȃ��Ȃ��C�Â��܂���Bδ�Ə�������
�ɋC�Â����ƂȂ̂ł���(�ȉ��ŇE���Ƃ���)�A���ꂪ�A�Ȃ��Ȃ��C�Â��܂���Bδ�Ə�������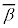 �Ə������Ƃɂ��C�Â��Ղ��Ȃ�Ǝv���܂��B���̂��߂ɏo��҂�(1)��u�����̂��낤�Ǝv���܂��B
�Ə������Ƃɂ��C�Â��Ղ��Ȃ�Ǝv���܂��B���̂��߂ɏo��҂�(1)��u�����̂��낤�Ǝv���܂��B
(1) 4��������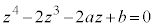 �͎����W���̕������Ȃ̂ŁAα�Cβ���Ƃ��Ɏ����łȂ����f���Ȃ�A
�͎����W���̕������Ȃ̂ŁAα�Cβ���Ƃ��Ɏ����łȂ����f���Ȃ�A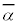 �C
�C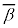 �����ɂȂ�A
�����ɂȂ�A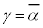 �C
�C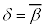 (
(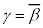 �C
�C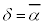 �ł�����)�Ƃ���ƁA
�ł�����)�Ƃ���ƁA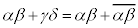 �͎���(x�Cy�������Ƃ��āA
�͎���(x�Cy�������Ƃ��āA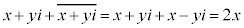 �͎����ł�)�ƂȂ�A����3�ɔ����܂��B
�͎����ł�)�ƂȂ�A����3�ɔ����܂��B α�Cβ�Cγ�Cδ�̂����A����1�����A���邢��3�������łȂ����f���A�Ƃ������Ƃ́A�����W���̕������ł͋N���蓾�܂���Bα�������łȂ����f���̉��Ȃ�A�����łȂ����f��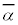 �����ɂȂ邩��ł��Bα�Cβ�Cγ�Cδ�����ׂĎ������̏ꍇ�A
�����ɂȂ邩��ł��Bα�Cβ�Cγ�Cδ�����ׂĎ������̏ꍇ�A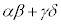 �������ł���A����3�ɔ����܂��B
�������ł���A����3�ɔ����܂��B
�ȏ���Aα�Cβ�Cγ�Cδ�̂����A���傤��2�������ł���A�c���2�݂͌��ɋ����ȕ��f���ł��B
(2) (1)�ɉ����āAα�Cβ���������ŁAγ�Cδ���݂��ɋ����ȕ��������A���邢�́Aγ�Cδ���������ŁAα�Cβ���݂��ɋ����ȕ��������Ƃ������Ƃ��N���蓾�܂���B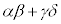 �������ɂȂ�A����3�ɔ����邩��ł��B
�������ɂȂ�A����3�ɔ����邩��ł��B �]���āAα�Cβ�̂ǂ��炩�������ő����������łȂ����f���Aγ�Cδ�̂ǂ��炩�������ő����������łȂ����f���ł��B
��蕶�̏����́Aα�Cβ�Ɋւ����Ώ��Aγ�Cδ�Ɋւ��đΏ̂Ȃ̂ŁAα�Cγ�������Aβ�Cδ���݂��ɋ����ȕ��f���Ƃ��A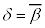 �Ƃ��܂�(α�Cδ�������Aβ�Cγ���݂��ɋ����ȕ��f���Ƃ��Ă������ł�)�Bα�Cβ�Cγ�C
�Ƃ��܂�(α�Cδ�������Aβ�Cγ���݂��ɋ����ȕ��f���Ƃ��Ă������ł�)�Bα�Cβ�Cγ�C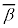 ���A4��������
���A4��������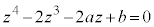 �̉��Ȃ̂ŁA���ƌW���̊W���A
�̉��Ȃ̂ŁA���ƌW���̊W���A 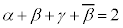 �@����@
�@����@
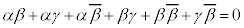 �@����A
�@����A
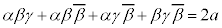 �@����B
�@����B
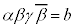 �@����C
�@����C�܂��A����3���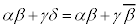 �̎�����0�ŋ�����0�łȂ����Ƃ��炱�̋�����c (c�F�����A
�̎�����0�ŋ�����0�łȂ����Ƃ��炱�̋�����c (c�F�����A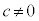 )�Ƃ����ƁA
)�Ƃ����ƁA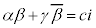 �@����D
�@����D
�A�ɂ��āAα�Cγ�͎����Ȃ̂ŁA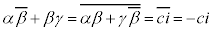 (���f�����Q��)���A
(���f�����Q��)���A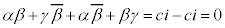 �ł����āA
�ł����āA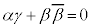 �@����Ep�Cq�������Ƃ��āA
�@����Ep�Cq�������Ƃ��āA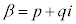 �Ƃ����A�D�ɑ������ƁA
�Ƃ����A�D�ɑ������ƁA ����āA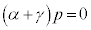 �C
�C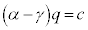
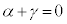 �܂���
�܂���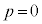
�ȉ��A�ꍇ�������Ē��ׂ܂��B
�E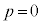 �̂Ƃ��A
�̂Ƃ��A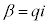 (β�͎����łȂ����f���Ȃ̂ŁA
(β�͎����łȂ����f���Ȃ̂ŁA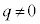 �ł�)
�ł�) �@��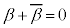 ���A
���A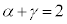 �@����F
�@����F
�B��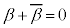 ���A
���A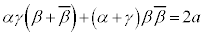
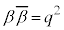 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA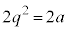 �@��
�@�� 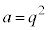 �E���A
�E���A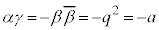 �@����G
�@����G
�C���A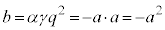
�E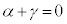 �̂Ƃ��A
�̂Ƃ��A �@���A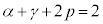 �@��
�@�� 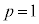 �@����H
�@����H
�B���A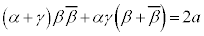
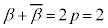 �C
�C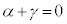 ���A
���A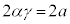 �@��
�@�� 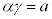 �@����I
�@����I
�E���A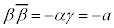 �@����J
�@����J
�D���A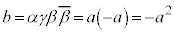
�ǂ���ɂ��Ă��A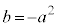 ......[��]
......[��]
(3) (2)�ɉ����āA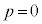 �̏ꍇ��
�̏ꍇ��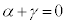 �̏ꍇ�ɕ����čl���܂��B(2)�Ɠ��l�ɁA
�̏ꍇ�ɕ����čl���܂��B(2)�Ɠ��l�ɁA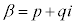 (p�Cq�F����)�Ƃ����܂��B
(p�Cq�F����)�Ƃ����܂��B �܂��A�F�F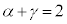 �C�G�F
�C�G�F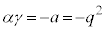 ���Aα�Cγ�́A2���������F
���Aα�Cγ�́A2���������F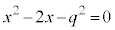 �̑��قȂ�2�������ł�(����1)�B
�̑��قȂ�2�������ł�(����1)�B
�� 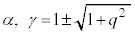
�Ƃ����ƁA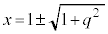 �C
�C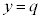
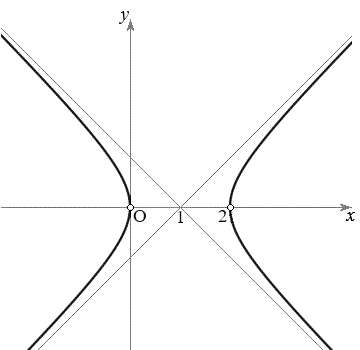 �E
�E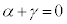 �̂Ƃ��A�H�F
�̂Ƃ��A�H�F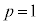 ���A
���A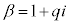 �ƂȂ�܂�(β�͎����łȂ����f���Ȃ̂�
�ƂȂ�܂�(β�͎����łȂ����f���Ȃ̂�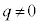 �ł�)�B�J�F
�ł�)�B�J�F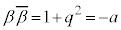 �ƇI�F
�ƇI�F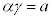 ���Aα�Cγ�́A2���������F
���Aα�Cγ�́A2���������F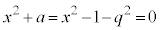 �̑��قȂ�2�������ł��B
�̑��قȂ�2�������ł��B�Ƃ����ƁA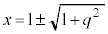 �C
�C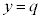
���f�����ʏ�ŁA�o�Ȑ�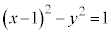 ��
��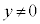 �̕����ł��B
�̕����ł��B �ǂ���̏ꍇ���A���f�����ʏ�ŁA�o�Ȑ�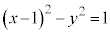 ��
��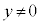 �̕����ŁA�}������ƁA�E�}����(���}��������)
�̕����ŁA�}������ƁA�E�}����(���}��������)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B