���嗝�n���w'19�N�O��[5]
�ȉ��̖₢�ɓ�����B
(1) n��1�ȏ�̐����Ƃ���Bx�ɂ��Ă̕�����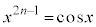 �́A������̎�����
�́A������̎�����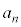 �������Ƃ������B
�������Ƃ������B (2) (1)�Œ�܂�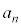 �ɑ��A
�ɑ��A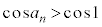 �������B
�������B (3) (1)�Œ�܂鐔��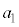 �C
�C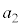 �C�������C
�C�������C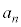 �C�������ɑ��A
�C�������ɑ��A �����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł��B(1)�C(2)����₱�����A(3)�̋Ɍ����l����Ƃ���ł́A�ǂ������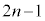 ��O�ʂɏo�����A�ƍl���邱�Ƃ��J�M�ł��B
��O�ʂɏo�����A�ƍl���邱�Ƃ��J�M�ł��B
(1) 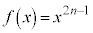 �́A
�́A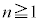 ���
���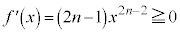 �ł���A���ׂĂ̎���x�ɂ��āA�P�������ł�(
�ł���A���ׂĂ̎���x�ɂ��āA�P�������ł�(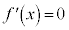 �ɂȂ�̂�
�ɂȂ�̂�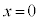 �̂�)�B
�̂�)�B 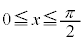 �ɂ����āA
�ɂ����āA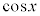 �͒P�������A
�͒P�������A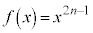 �͒P�������A
�͒P�������A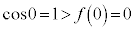 �C
�C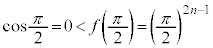 ���A������
���A������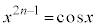 �́A
�́A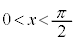 �͈̔͂ɂ�����̎������������܂��B�����
�͈̔͂ɂ�����̎������������܂��B�����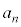 �Ƃ��܂��B���(��)
�Ƃ��܂��B���(��)�ȏ���Ax�ɂ��Ă̕�����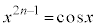 �́A������̎�����
�́A������̎�����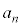 �������܂��B
�������܂��B ���D�͈� �������Ƃ�A
�������Ƃ�A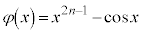 �C
�C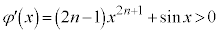 ���
���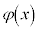 �͒P�������A
�͒P�������A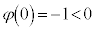 �C
�C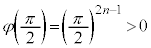 �C���Ԓl�̒藝���A
�C���Ԓl�̒藝���A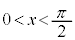 �ɂ����ĕ�����
�ɂ����ĕ�����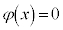 �͂���1�̎����������A�Ƃ���ق������ꂢ�ł��B
�͂���1�̎����������A�Ƃ���ق������ꂢ�ł��B
(2) (1)��(��)���A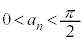 �ł��B
�ł��B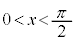 �ɂ�����
�ɂ�����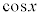 �͒P�������Ȃ̂ŁA
�͒P�������Ȃ̂ŁA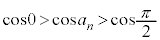 �C�܂�A
�C�܂�A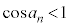 �@����@
�@����@ �Ƃ���ŁA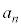 �͕�����
�͕�����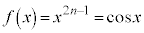 �̉��Ȃ̂ŁA
�̉��Ȃ̂ŁA 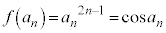 �@����A
�@����A�܂��A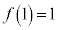 �Ƈ@�C�A���A
�Ƈ@�C�A���A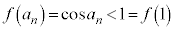 �C
�C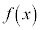 �͒P�������Ȃ̂ŁA
�͒P�������Ȃ̂ŁA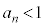 �@����B
�@����B
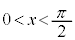 �ɂ�����
�ɂ�����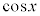 �͒P�������ł���A
�͒P�������ł���A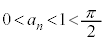 ���A
���A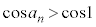 �@����C
�@����C
(3) �@�C�C���A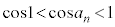
�A���A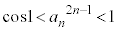 �C�����A
�C�����A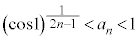 �@����D
�@����D
�����ŁA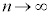 �Ƃ���ƁA
�Ƃ���ƁA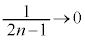 (����̋Ɍ����Q��)���A
(����̋Ɍ����Q��)���A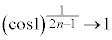
�D�ɂ����āA�͂��݂����̌������A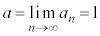 ......[��]�@����E
......[��]�@����E
�A��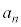 �������āA
�������āA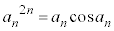 �C����āA
�C����āA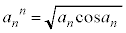 �@����F
�@����F
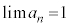 ���A
���A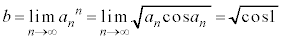 ......[��]�F���A
......[��]�F���A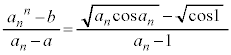 �@����G
�@����G
�G�̌`����A���ϒl�̒藝�̗��p���l���܂��B
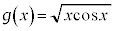 �Ƃ����ƁA�G�́A
�Ƃ����ƁA�G�́A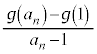 �ƂȂ�܂��B
�ƂȂ�܂��B 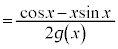 �@����H
�@����H�B���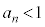 �ł����A���ϒl�̒藝���A
�ł����A���ϒl�̒藝���A 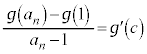 �C
�C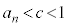 �@����I
�@����I��������c�����݂��܂��B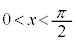 �ɂ����āA
�ɂ����āA ����āA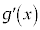 ��
��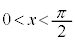 �ɂ����ĒP�������ŁA
�ɂ����ĒP�������ŁA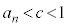 ���A
���A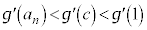 �ł��B�I���A
�ł��B�I���A �����ŁA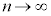 �Ƃ���ƁA
�Ƃ���ƁA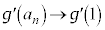 �C�͂��݂����̌������A
�C�͂��݂����̌������A �H���A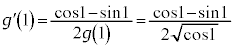
�� 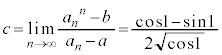 ......[��]
......[��] ���D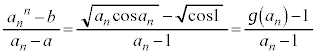 �ŁA
�ŁA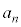 ��x�ɒu�������āA
��x�ɒu�������āA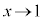 �Ƃ���A
�Ƃ���A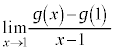 �������W��
�������W��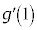 �̂��ƂȂ̂ŁA���̌��ʂ͓��R�ł��B
�̂��ƂȂ̂ŁA���̌��ʂ͓��R�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 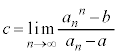
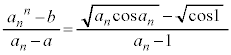 �@����G
�@����G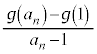 �ƂȂ�܂��B
�ƂȂ�܂��B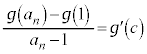 �C
�C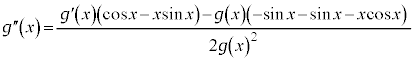
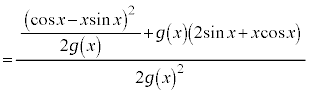
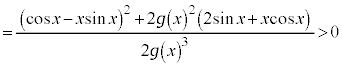
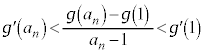
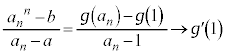
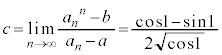 ......[��]
......[��]