���嗝�n���w'21�N�O��[2]
���f��a�Cb�Cc�ɑ��Đ���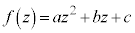 ���l����Bi�������P�ʂƂ���B
���l����Bi�������P�ʂƂ���B
(1) α�Cβ�Cγ�f���Ƃ���B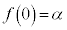 �C
�C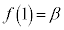 �C
�C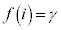 �����藧�Ƃ��Aa�Cb�Cc�����ꂼ��α�Cβ�Cγ�ŕ\���B
�����藧�Ƃ��Aa�Cb�Cc�����ꂼ��α�Cβ�Cγ�ŕ\���B (2) 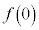 �C
�C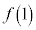 �C
�C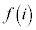 ���������1�ȏ�2�ȉ��̎����ł���Ƃ��A
���������1�ȏ�2�ȉ��̎����ł���Ƃ��A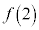 �̂Ƃ肤��͈͂f�����ʏ�ɐ}������B
�̂Ƃ肤��͈͂f�����ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�͑�1��Ɠ����悤�Ȃ��ƂɂȂ��Ă��܂��܂����A������͓������̂�3�ł��B
(1) 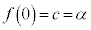 �@����@�C
�@����@�C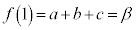 �@����A�C
�@����A�C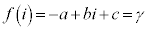 �@����B
�@����B �A�{�B���A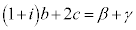 �C�@�������A
�C�@�������A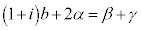 �C
�C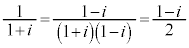 (���f���̌v�Z���Q��)���A
(���f���̌v�Z���Q��)���A
�� 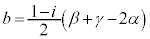 ����Ƈ@���A�֑�����A
����Ƈ@���A�֑�����A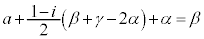
(2) 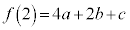 �C(1)�̌��ʂ��A
�C(1)�̌��ʂ��A 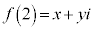 (x�Cy�͎���)�Ƃ����ƁA
(x�Cy�͎���)�Ƃ����ƁA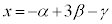 �@����C�C
�@����C�C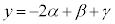 �@����D
�@����D3���������̂ł͑�ςȂ̂ŁA2�����1�������������čl���܂��B
�C�{�D���A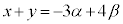 �@��
�@�� 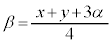 �C
�C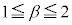 ���A
���A 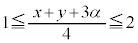 �C
�C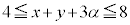
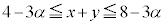 (���̓�����
(���̓�����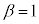 �̂Ƃ��C�E�̓�����
�̂Ƃ��C�E�̓�����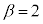 �̂Ƃ�)
�̂Ƃ�)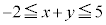 �C�܂�A
�C�܂�A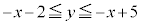 (���̓�����
(���̓�����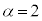 ����
����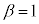 �̂Ƃ��A�E�̓�����
�̂Ƃ��A�E�̓�����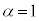 ����
����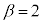 �̂Ƃ�)�@����E
�̂Ƃ�)�@����E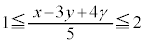 �C
�C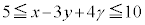
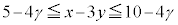 (���̓�����
(���̓�����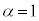 �̂Ƃ��A�E�̓�����
�̂Ƃ��A�E�̓�����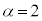 �̂Ƃ�)
�̂Ƃ�)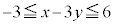 �C�܂�A
�C�܂�A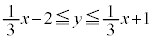 (���̓�����
(���̓�����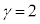 ����
����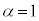 �̂Ƃ��A�E�̓�����
�̂Ƃ��A�E�̓�����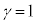 ����
����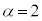 �̂Ƃ�)�@����F
�̂Ƃ�)�@����F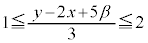 �C
�C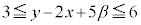
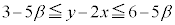 (���̓�����
(���̓�����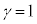 �̂Ƃ��A�E�̓�����
�̂Ƃ��A�E�̓�����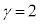 �̂Ƃ�)
�̂Ƃ�)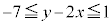 �C�܂�A
�C�܂�A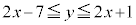 (���̓�����
(���̓�����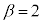 ����
����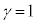 �̂Ƃ��A�E�̓�����
�̂Ƃ��A�E�̓�����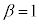 ����
����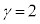 �̂Ƃ�)�@����G
�̂Ƃ�)�@����G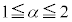 ����
����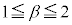 ����
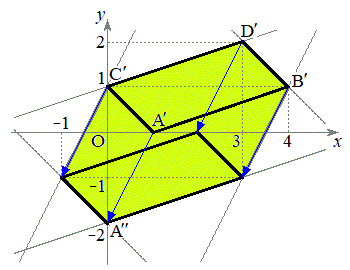
����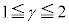 ���A���߂�͈͂́A�E���F���G�ł��B�}������ƉE�}���ΐF���F��(���E�����܂�)�B(�s�����̕\���̈����Q��)
���A���߂�͈͂́A�E���F���G�ł��B�}������ƉE�}���ΐF���F��(���E�����܂�)�B(�s�����̕\���̈����Q��)
�NjL�D�E���}�ɁA���߂�͈͂̋��E����A���_�ŁAα�Cβ�Cγ���ǂ̂悤�Ȓl���Ƃ邩�A�������Ă����܂��B�ǂ����āA�E��}�̂悤�Ȕ͈͂ɂȂ邩���킩��Ǝv���܂��B
 ���C�C�C�D���A
���C�C�C�D���A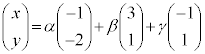 �ƌ���ƁA
�ƌ���ƁA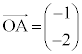 �C
�C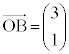 �C
�C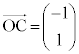 �C
�C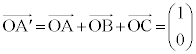 �C
�C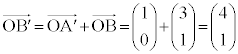 �C
�C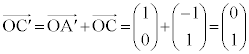 �C
�C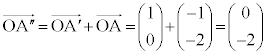 �Ƃ��āA
�Ƃ��āA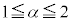 ���Aα��1����2�܂œ����Ƃ��ɁA
���Aα��1����2�܂œ����Ƃ��ɁA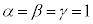 �ƂȂ�_
�ƂȂ�_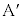 ��1���_�Ƃ���
��1���_�Ƃ���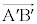 �C
�C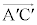 �ō���镽�s�l�ӌ`
�ō���镽�s�l�ӌ`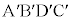 (
(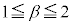 �C
�C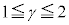 �C
�C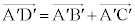 �C�x�N�g����1���Ɨ����Q��)���A���_
�C�x�N�g����1���Ɨ����Q��)���A���_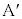 ��
��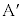 ����
����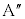 �܂œ����悤�ɕ��s�ړ�(
�܂œ����悤�ɕ��s�ړ�(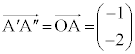 �̕�����)���Ēʉ߂��镔�������߂�͈�(�E�}���ΐF����)�ɂȂ�܂��B
�̕�����)���Ēʉ߂��镔�������߂�͈�(�E�}���ΐF����)�ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 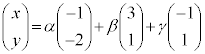 �ƌ���ƁA
�ƌ���ƁA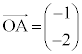 �C
�C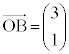 �C
�C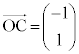 �C
�C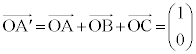 �C
�C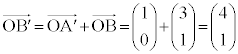 �C
�C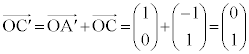 �C
�C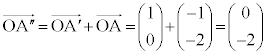 �Ƃ��āA
�Ƃ��āA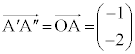 �̕�����)���Ēʉ߂��镔�������߂�͈�(�E�}���ΐF����)�ɂȂ�܂��B
�̕�����)���Ēʉ߂��镔�������߂�͈�(�E�}���ΐF����)�ɂȂ�܂��B