���嗝�n���w'21�N�O��[6]
�萔b�Cc�Cp�Cq�Cr�ɑ��A
��x�ɂ��Ă̍P�����ł���Ƃ���B
(1) 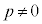 �ł���Ƃ��Aq�Cr��p�Cb�ŕ\���B
�ł���Ƃ��Aq�Cr��p�Cb�ŕ\���B (2) 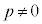 �Ƃ���Bb�Cc���萔a��p����
�Ƃ���Bb�Cc���萔a��p���� 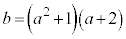 �C
�C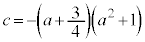
�ƕ\����Ă���Ƃ��A�L�������W���Ƃ���t �ɂ��Ă̐��� ��
�� ��
�� �������̂�1�g���߂�B
(3) a�𐮐��Ƃ���Bx��4����
���L�������W���Ƃ���2�����̐ςɈ��������ł���悤��a�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�́A(1)(2)�𗘗p���čl���܂����A�d�|�������G�ŁA�ǂ�����悢���A�Ƃ������Ǝ��̂��l���ɂ������ł��B���j�������Ă��A���Ƃ������������҂��Ă���̂ŁA�אS�̒��ӂ��K�v�ł��B
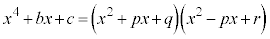 �@����@
�@����@
�@���ӂƊe���̌W�����r����ƁA
�A���A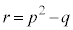 �@����D
�@����D
�B�ɑ�����āA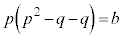 �@��
�@�� 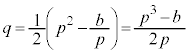 ......[��]�D�ɑ�����āA
......[��]�D�ɑ�����āA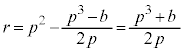 ......[��]
......[��] (2) (1)�̌��ʂ��C�ɑ�����āA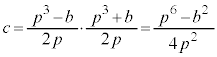
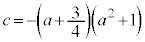 ���A
���A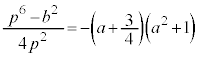
�� 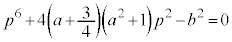
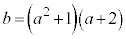 ���A
���A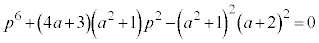 �@����E
�@����E
��蕶�̎��F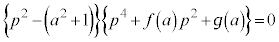 �@����F�@�̍��ӂ��W�J�����
�@����F�@�̍��ӂ��W�J������E�Ɗe���̌W�����r����ƁA
�G���A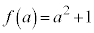
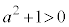 �Ȃ̂ŇI���A
�Ȃ̂ŇI���A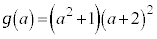
�������H���E�ӂɑ������ƁA �H�����ӂɂȂ�̂ŁA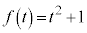 �C
�C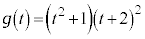 ......[��]�@�G�C�H���A�����ɓK���̂͂���1�g�ł����āA����ȊO�ɂ͂���܂���B
......[��]�@�G�C�H���A�����ɓK���̂͂���1�g�ł����āA����ȊO�ɂ͂���܂���B (3) b�Cc��(2)�̖�蕶���ɗ^�����Ă�����̂��Ƃ��āA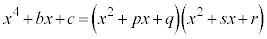 �ƈ��������ł����Ƃ��܂��B
�ƈ��������ł����Ƃ��܂��B �E�ӂ�W�J����ƁA
�W�����r���āA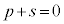 �C
�C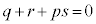
�� 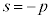 �C
�C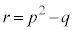
������A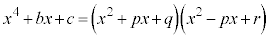
�Ƃ����`�Ɉ��������ł��܂�(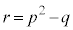 �͇D�Ɠ���)�B
�͇D�Ɠ���)�B 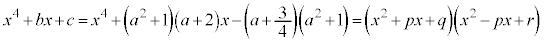 �@����J
�@����J�����������ł���Ƃ���ƁA(2)���A�F�ɂ�����L����p���߂�A(1)�̌��ʂ�p���ėL����q�Cr�����߂邱�Ƃɂ����������ł���킯�ł��B
�F���A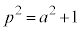 �@����K�@�܂��́A
�@����K�@�܂��́A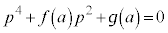 �@����L
�@����L �E�K�ƂȂ�Ƃ��A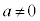 ���Ƃ��āAp���L�����A�܂�
���Ƃ��āAp���L�����A�܂�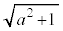 (
(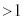 )���L�������Ɖ��肷��ƁAm�Cn���݂��ɑf�Ȏ��R���Ƃ��āA
)���L�������Ɖ��肷��ƁAm�Cn���݂��ɑf�Ȏ��R���Ƃ��āA �Ƃ����܂��B2�悵��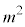 ��������ƁA
��������ƁA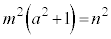 �@����M
�@����M
������An��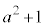 �̔{���ŁA
�̔{���ŁA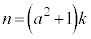 �Ƃ����܂��B�M�ɑ������ƁA
�Ƃ����܂��B�M�ɑ������ƁA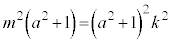
�� 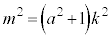 ����́Am��
����́Am��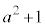 �̔{���ł��邱�Ƃ��Ӗ����Am�Cn���݂��ɑf�ł͂Ȃ��Ȃ�A
�̔{���ł��邱�Ƃ��Ӗ����Am�Cn���݂��ɑf�ł͂Ȃ��Ȃ�A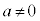 �ł�
�ł�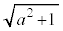 �͖������ɂȂ��Ă��܂��܂��B
�͖������ɂȂ��Ă��܂��܂��B
�]���āA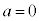 �C
�C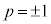 �ł��B
�ł��B
���̂Ƃ��A(2)�̖�蕶���̎����A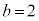 �C
�C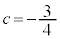 �ŁA(1)�̌��ʂ�p���āA
�ŁA(1)�̌��ʂ�p���āA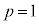 �̂Ƃ��A
�̂Ƃ��A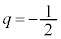 �C
�C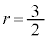 �C�܂��́A
�C�܂��́A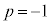 �̂Ƃ��A
�̂Ƃ��A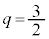 �C
�C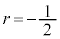 �ƂȂ�A������ɂ��Ă��J��
�ƂȂ�A������ɂ��Ă��J�� �ƗL�������W���Ƃ���2�����̐ς����������ł��܂��B �E�L�ƂȂ�Ƃ��A�L��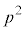 �Ɋւ���2���������Ƃ݂�Ǝ����������̂ŁA���ʎ�D�ɂ��āA
�Ɋւ���2���������Ƃ݂�Ǝ����������̂ŁA���ʎ�D�ɂ��āA (2)�̌��ʂ��A
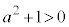 �Ȃ̂ŁA
�Ȃ̂ŁA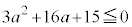 �C�����A
�C�����A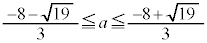
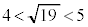 ���A
���A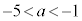 �C����āA
�C����āA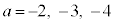 �ł��B�܂��L�������āA
�ł��B�܂��L�������āA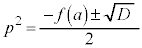 �ł��B
�ł��B(i) 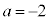 �̂Ƃ��A
�̂Ƃ��A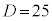 �C
�C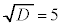 �C
�C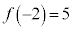 �C
�C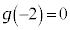 �C
�C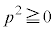 ���A
���A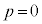 �ł��B
�ł��B ���̂Ƃ��A(2)�̖�蕶���̎����A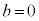 �C
�C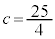 �ƂȂ�܂����A�A���
�ƂȂ�܂����A�A���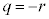 �C�C���
�C�C���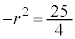 �C��������L����q�Cr�͑��݂��܂���B�܂�A���̂Ƃ��J�F
�C��������L����q�Cr�͑��݂��܂���B�܂�A���̂Ƃ��J�F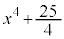 �͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B
�͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B (ii) 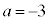 �̂Ƃ��A
�̂Ƃ��A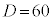 �C
�C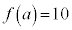 �C���̂Ƃ���
�C���̂Ƃ���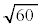 ���������ŁA
���������ŁA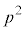 �͗L�����ɂȂ炸�A
�͗L�����ɂȂ炸�A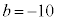 �C
�C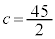 �ƂȂ�܂����A�J�F
�ƂȂ�܂����A�J�F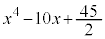 �͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B�B
�͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B�B (iii) 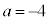 �̂Ƃ��A
�̂Ƃ��A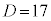 �C
�C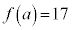 �C���̂Ƃ���
�C���̂Ƃ���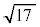 ���������ŁA
���������ŁA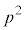 �͗L�����ɂȂ炸�A
�͗L�����ɂȂ炸�A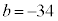 �C
�C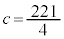 �ƂȂ�܂����A�J�F
�ƂȂ�܂����A�J�F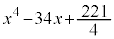 �͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B
�͗L�����W����2�����̐ς̌`�ɂ͈��������ł��܂���B �ȏ���A��蕶��4�������L�������W���Ƃ���2�����̐ςɈ��������ł���悤��a�́A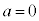 ......[��]���D
......[��]���D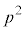 �Ɋւ���2���������L�́A�����Ȃ��Ă��A
�Ɋւ���2���������L�́A�����Ȃ��Ă��A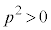 �̂Ƃ��A
�̂Ƃ��A �ł����āA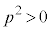 �͈̔͂Ɏ��������������A�������͂������Ƃ��Ă�
�͈̔͂Ɏ��������������A�������͂������Ƃ��Ă�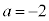 �̂Ƃ���
�̂Ƃ���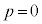 �Ɍ����܂��B����ɋC�Â��A��L��(ii)
�Ɍ����܂��B����ɋC�Â��A��L��(ii)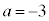 �C(iii)
�C(iii)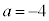 �̏ꍇ�����͕s�v�ɂȂ�܂��B
�̏ꍇ�����͕s�v�ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 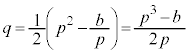 ......[��]
......[��]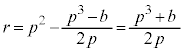 ......[��]
......[��]