東大理系数学'22年前期[3]
Oを原点とする座標平面上で考える。座標平面上の2点S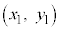 ,T
,T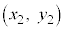 に対し、点Sが点Tから十分離れているとは、
に対し、点Sが点Tから十分離れているとは、
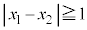 または
または 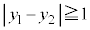
不等式
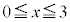 ,
,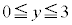
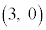 ,B
,B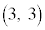 を考える。さらに、次の条件(i),(ii)をともに満たす点Pをとる。
を考える。さらに、次の条件(i),(ii)をともに満たす点Pをとる。
(i) 点Pは領域Dの点であり、かつ、放物線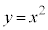 上にある。(ii) 点Pは、3点O,A,Bのいずれからも十分離れている。
上にある。(ii) 点Pは、3点O,A,Bのいずれからも十分離れている。 点Pのx座標をaとする。
(1) aのとりうる値の範囲を求めよ。
(2) 次の条件(iii),(iv)をともに満たす点Qが存在しうる範囲の面積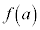 を求めよ。
を求めよ。 (iii) 点Qは領域Dの点である。
(iv) 点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3) aは(1)で求めた範囲を動くとする。(2)の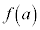 を最小にするaの値を求めよ。
を最小にするaの値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 ややこしいですが、計算ミスに注意して、確実にものにしたい問題です。なお、絶対値記号を含む1次方程式・1次不等式を参照してください。
点Pが、
点Oから十分離れているので、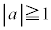 または
または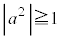
点Aから十分離れているので、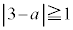 または
または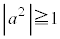
点Bから十分離れているので、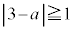 または
または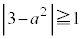
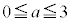 の範囲で考えて、以上より、
の範囲で考えて、以上より、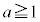 かつ "
かつ "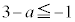 または
または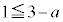 " かつ "
" かつ "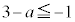 または
または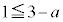 または
または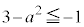 または
または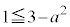 "即ち、
"即ち、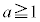 かつ "
かつ "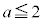 " かつ "
" かつ "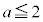 または
または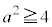 "即ち、
"即ち、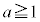 かつ
かつ 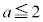
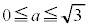 と合わせて、
と合わせて、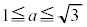 ......[答]
......[答] 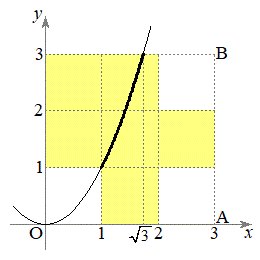 別解.上記は不等式で解答しましたが、条件(ii)を満たす領域を図示(右図黄色着色部、境界線含む)して、その領域内の放物線
別解.上記は不等式で解答しましたが、条件(ii)を満たす領域を図示(右図黄色着色部、境界線含む)して、その領域内の放物線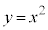 の部分(
の部分(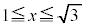 に存在します。右図太線部分)を考える方が容易です。
に存在します。右図太線部分)を考える方が容易です。
(2) Qの座標を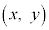 とすると、点Qが領域D内の点であることから、
とすると、点Qが領域D内の点であることから、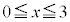 ,
,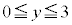
点Qが、
点Oから十分離れているので、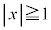 または
または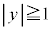
点Aから十分離れているので、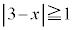 または
または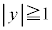
点Bから十分離れているので、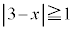 または
または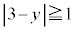
点Pから十分離れているので、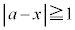 または
または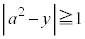
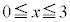 ,
,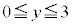 の範囲で考えて、以上より、"
の範囲で考えて、以上より、"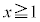 または
または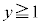 " かつ "
" かつ "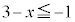 または
または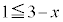 または
または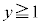 " かつ "
" かつ "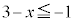 または
または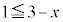 または
または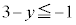 または
または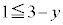 " かつ "
" かつ "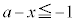 または
または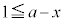 または
または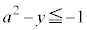 または
または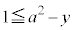 "即ち、"
"即ち、"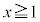 または
または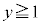 " かつ "
" かつ "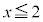 または
または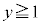 " かつ "
" かつ "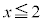 または
または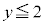 " かつ "
" かつ "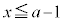 または
または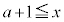 または
または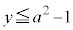 または
または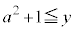 "不等式がたくさん出てきますが、このうち問題になるのは、
"不等式がたくさん出てきますが、このうち問題になるのは、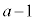 ,
,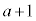 ,
,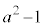 ,
,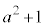 です。(1)より
です。(1)より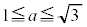 ですが、
ですが、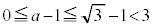 ,
,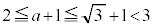 ,
,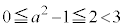 はPが領域D内にあるときには、x,yの範囲の限界の値として、問題なしです。
はPが領域D内にあるときには、x,yの範囲の限界の値として、問題なしです。
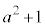 については、
については、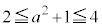 となるので、Pが領域D内にあっても、x,yの範囲の限界の値が、領域Dに入らない場合があります。そこで、
となるので、Pが領域D内にあっても、x,yの範囲の限界の値が、領域Dに入らない場合があります。そこで、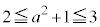 になる場合と
になる場合と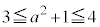 になる場合とで、場合分けします。
になる場合とで、場合分けします。
・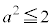 のときは、
のときは、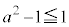 ,
,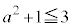 となるので、
となるので、 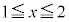 かつ
かつ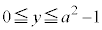 の面積は、
の面積は、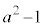
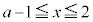 かつ
かつ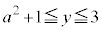 の面積は、
の面積は、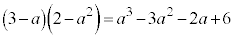
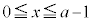 かつ
かつ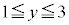 の面積は、
の面積は、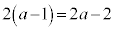
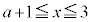 かつ
かつ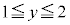 の面積は、
の面積は、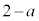
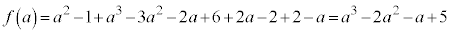
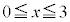 かつ
かつ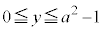 の面積が
の面積が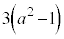 ,ここから、
,ここから、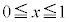 かつ
かつ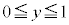 の面積1の正方形と
の面積1の正方形と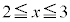 かつ
かつ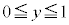 の面積1の正方形を除いて、
の面積1の正方形を除いて、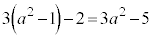
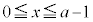 かつ
かつ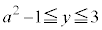 の面積は、
の面積は、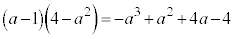
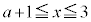 かつ
かつ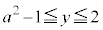 の面積は、
の面積は、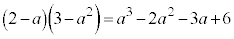

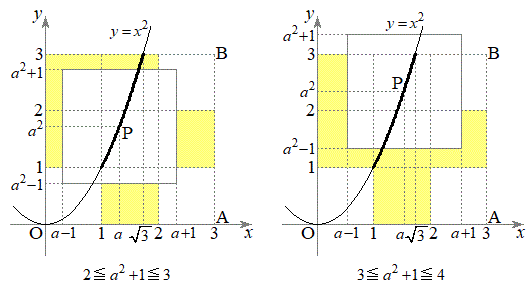 別解.(2)も、不等式で考察を進めても、面積を計算するときには、重複して計算しないように、それぞれ長方形を描いて確認する必要があるので、最初から条件(ii)を満たす領域から、点Pから十分に離れていない領域(点P
別解.(2)も、不等式で考察を進めても、面積を計算するときには、重複して計算しないように、それぞれ長方形を描いて確認する必要があるので、最初から条件(ii)を満たす領域から、点Pから十分に離れていない領域(点P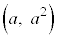 を中心とし各辺がx軸またはy軸に平行である1辺2の正方形の内側)を除いた部分(右図黄色着色部、境界線含む)を図示して考える方が安全確実です。上記で述べたように、
を中心とし各辺がx軸またはy軸に平行である1辺2の正方形の内側)を除いた部分(右図黄色着色部、境界線含む)を図示して考える方が安全確実です。上記で述べたように、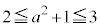 となる場合と
となる場合と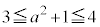 となる場合で分けて図示して考えることになります。
となる場合で分けて図示して考えることになります。
(3) 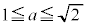 のとき、
のとき、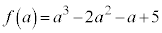
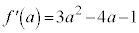 ,
,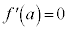 とすると、
とすると、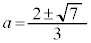 ,
,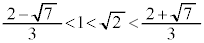 より、
より、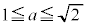 において
において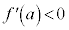 ,この範囲で
,この範囲で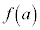 は単調減少で、
は単調減少で、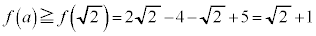 (3次関数の最大最小を参照)
(3次関数の最大最小を参照)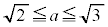 のとき、
のとき、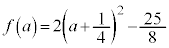 ,軸の位置:
,軸の位置: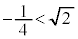 より、
より、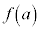 は
は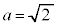 で最小(2次関数の最大最小を参照)です。
で最小(2次関数の最大最小を参照)です。
以上より、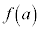 を最小にするaの値は、
を最小にするaの値は、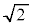 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。