東京大学理系2022年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の関数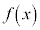 を考える。
を考える。
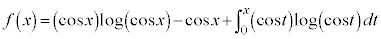 (
(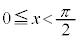 )
)(1) 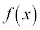 は区間
は区間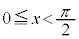 において最小値を持つことを示せ。
において最小値を持つことを示せ。 (2) 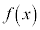 の区間
の区間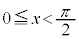 における最小値を求めよ。
における最小値を求めよ。 [解答へ]
[2] 数列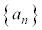 を次のように定める。
を次のように定める。
(1) 正の整数nが3の倍数のとき、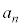 は5の倍数となることを示せ。
は5の倍数となることを示せ。 (2) k,nを正の整数とする。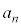 が
が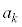 の倍数となるための必要十分条件をk,nを用いて表せ。
の倍数となるための必要十分条件をk,nを用いて表せ。 (3) 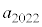 と
と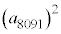 の最大公約数を求めよ。
の最大公約数を求めよ。
[解答へ]
[3] Oを原点とする座標平面上で考える。座標平面上の2点S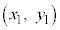 ,T
,T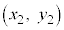 に対し、点Sが点Tから十分離れているとは、
に対し、点Sが点Tから十分離れているとは、
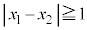 または
または 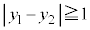
不等式
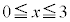 ,
,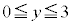
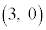 ,B
,B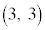 を考える。さらに、次の条件(i),(ii)をともに満たす点Pをとる。
を考える。さらに、次の条件(i),(ii)をともに満たす点Pをとる。
(i) 点Pは領域Dの点であり、かつ、放物線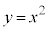 上にある。(ii) 点Pは、3点O,A,Bのいずれからも十分離れている。
上にある。(ii) 点Pは、3点O,A,Bのいずれからも十分離れている。 点Pのx座標をaとする。
(1) aのとりうる値の範囲を求めよ。
(2) 次の条件(iii),(iv)をともに満たす点Qが存在しうる範囲の面積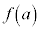 を求めよ。
を求めよ。 (iii) 点Qは領域Dの点である。
(iv) 点Qは、4点O,A,B,Pのいずれからも十分離れている。
(3) aは(1)で求めた範囲を動くとする。(2)の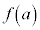 を最小にするaの値を求めよ。
を最小にするaの値を求めよ。 [解答へ]
[4] 座標平面上の曲線
C: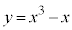
(1) 座標平面上のすべての点Pが次の条件(i)を満たすことを示せ。
(i) 点Pを通る直線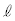 で、曲線Cと相異なる3点で交わるものが存在する。
で、曲線Cと相異なる3点で交わるものが存在する。 (2) 次の条件(ii)を満たす点Pのとりうる範囲を座標平面上に図示せよ。
(ii) 点Pを通る直線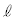 で、曲線Cと相異なる3点で交わり、かつ、直線
で、曲線Cと相異なる3点で交わり、かつ、直線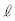 と曲線Cで囲まれた2つの部分の面積が等しくなるものが存在する。
と曲線Cで囲まれた2つの部分の面積が等しくなるものが存在する。 [解答へ]
[5] 座標空間内の点A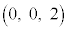 と点B
と点B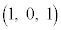 を結ぶ線分をz軸のまわりに1回転させて得られる曲面をSとする。S上の点Pとxy平面上の点Qが
を結ぶ線分をz軸のまわりに1回転させて得られる曲面をSとする。S上の点Pとxy平面上の点Qが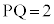 を満たしながら動くとき、線分PQの中点が通過しうる範囲をKとする。Kの体積を求めよ。
を満たしながら動くとき、線分PQの中点が通過しうる範囲をKとする。Kの体積を求めよ。
[解答へ]
[6] Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル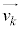 を
を
と定める。投げたとき表と裏がどちらも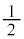 の確率で出るコインをN回投げて、座標平面上に点
の確率で出るコインをN回投げて、座標平面上に点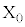 ,
,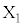 ,
,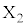 ,・・・,
,・・・,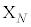 を以下の規則(i),(ii)に従って定める。
を以下の規則(i),(ii)に従って定める。
(i) 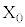 はOにある。
はOにある。 (ii) nを1以上N以下の整数とする。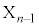 が定まったとし、
が定まったとし、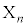 を次のように定める。
を次のように定める。 ・n回目のコイン投げで表が出た場合、
により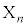 を定める。ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。
を定める。ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。 ・n回目のコイン投げで裏が出た場合、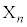 を
を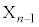 と定める。
と定める。 (1) 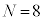 とする。
とする。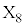 がOにある確率を求めよ。
がOにある確率を求めよ。 (2) 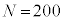 とする。
とする。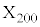 がOにあり、かつ、合計200回のコイン投げで表がちょうどr回出る確率を
がOにあり、かつ、合計200回のコイン投げで表がちょうどr回出る確率を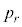 とおく。ただし
とおく。ただし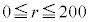 である。
である。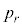 を求めよ。また
を求めよ。また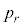 が最大となるrの値を求めよ。
が最大となるrの値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。