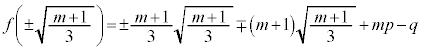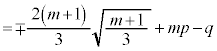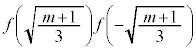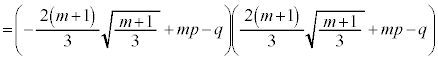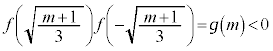���嗝�n���w'22�N�O��[4]
���W���ʏ�̋Ȑ�
C�F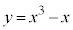
(1) ���W���ʏ�̂��ׂĂ̓_P�����̏���(i)�������Ƃ������B
(i) �_P��ʂ钼��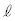 �ŁA�Ȑ�C�Ƒ��قȂ�3�_�Ō������̂����݂���B
�ŁA�Ȑ�C�Ƒ��قȂ�3�_�Ō������̂����݂���B (2) ���̏���(ii)�����_P�̂Ƃ肤��͈͂����W���ʏ�ɐ}������B
(ii) �_P��ʂ钼��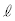 �ŁA�Ȑ�C�Ƒ��قȂ�3�_�Ō����A���A����
�ŁA�Ȑ�C�Ƒ��قȂ�3�_�Ō����A���A���� �ƋȐ�C�ň͂܂ꂽ2�̕����̖ʐς��������Ȃ���̂����݂���B
�ƋȐ�C�ň͂܂ꂽ2�̕����̖ʐς��������Ȃ���̂����݂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������3���Ȑ��ň͂�2�̕����̖ʐς��������Ȃ�̂́A�������ϋȓ_��ʂ�ꍇ�ł��B3���Ȑ����ϋȓ_�ɂ��đΏ̂�����ł��B�������Ŏ��Ԃɒǂ���ꍇ�A���_�o��ł��̎���(3�����̃O���t���Q��)��p���ĉ��邱�Ƃ��ł��܂��B
(1) �_P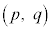 ��ʂ钼���F
��ʂ钼���F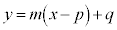 �@����@
�@����@ C�F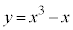 �ƘA������ƁA
�ƘA������ƁA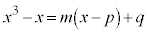
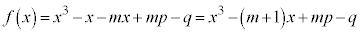 �@����A�@�Ƃ����ƁA
�@����A�@�Ƃ����ƁA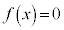 �����قȂ�3���������������́A�ɑ�l�E�ɏ��l��0 (3�����������Q��)
�����قȂ�3���������������́A�ɑ�l�E�ɏ��l��0 (3�����������Q��)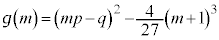 �Ƃ����ƁA
�Ƃ����ƁA ��3�����ŁA
��3�����ŁA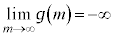 ���A�C�ӂ̎���p�Cq�ɑ��āA
���A�C�ӂ̎���p�Cq�ɑ��āA�ƂȂ�m (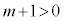 )�����݂��܂��B����āA���W���ʏ�̂��ׂĂ̓_P������(i)�����܂��B
)�����݂��܂��B����āA���W���ʏ�̂��ׂĂ̓_P������(i)�����܂��B
(2) (1)�ɂ��A���W���ʏ�̔C�ӂ̓_����Ȑ�C�Ƒ��قȂ�3��_��L���钼�����������Ƃ��ł���̂ŁA���̒������@�Ƃ��āAC�F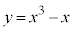 �ƘA������ƁA�A��
�ƘA������ƁA�A��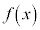 �ɂ��āA3���������F
�ɂ��āA3���������F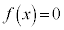 ��3�̑��قȂ������α�Cβ�Cγ (
��3�̑��قȂ������α�Cβ�Cγ (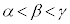 )�������A
)�������A �ł��B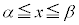 �ɂ�����
�ɂ�����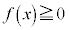 �C
�C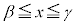 �ɂ�����
�ɂ�����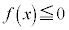 ���A�Ȑ�C�ƒ����@�Ƃň͂�2�̕������ʐ����������̂ŁA
���A�Ȑ�C�ƒ����@�Ƃň͂�2�̕������ʐ����������̂ŁA �B���A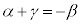 �Ȃ̂ŁA
�Ȃ̂ŁA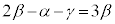 �C����āA
�C����āA 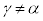 ���A
���A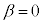 (�܂�A2�̕����̖ʐς��������Ƃ��A�����͕ϋȓ_�A�{��ł͌��_�A��ʂ�܂�)�ł��B���̂Ƃ��A�B���A
(�܂�A2�̕����̖ʐς��������Ƃ��A�����͕ϋȓ_�A�{��ł͌��_�A��ʂ�܂�)�ł��B���̂Ƃ��A�B���A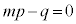 �@��
�@�� 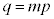 �@����C
�@����C
�����@�́A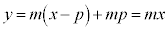
�܂��A�B��2�Ԗڂ̎���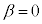 �Ƃ��āA
�Ƃ��āA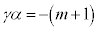
�B��1�Ԗڂ̎���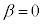 �Ƃ��āA
�Ƃ��āA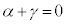 ���A
���A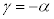 �C�܂��A
�C�܂��A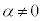 �C����āA
�C����āA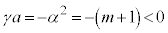 �@����D
�@����D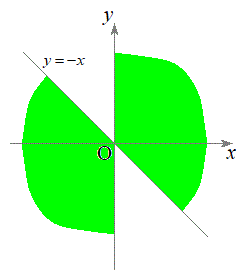
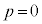 �C
�C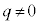 �̂Ƃ��A�ϋȓ_�ƌ��Ԓ���(y��)�͋Ȑ�C�ƁA��蕶���ɂ���2�̕��������Ȃ��̂ŁA
�̂Ƃ��A�ϋȓ_�ƌ��Ԓ���(y��)�͋Ȑ�C�ƁA��蕶���ɂ���2�̕��������Ȃ��̂ŁA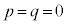 (���_)�̏ꍇ��������
(���_)�̏ꍇ�������� �ł��B
�ł��B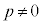 �Ƃ��ćC���
�Ƃ��ćC���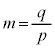 �C�D���A
�C�D���A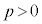 �̂Ƃ��A
�̂Ƃ��A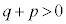 �C�܂�A
�C�܂�A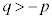
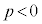 �̂Ƃ��A
�̂Ƃ��A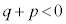 �C�܂�A
�C�܂�A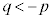
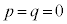 �̂Ƃ��́A
�̂Ƃ��́A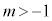 �ł���·D�����̂ŁA����(ii)�������������݂��܂��B
�ł���·D�����̂ŁA����(ii)�������������݂��܂��B
�_P�̂Ƃ肤��͈͂�}������ƉE�}���ΐF���F��(���_���܂݁A���_�ȊO�̋��E���������)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B