3次関数のグラフ 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
3次関数: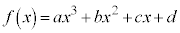 (
(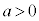 ) ・・・・① のグラフを調べます。
) ・・・・① のグラフを調べます。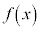 を微分すると、
を微分すると、
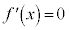 とすると、
とすると、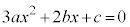 ・・・②
・・・②
この2次方程式の判別式: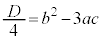 として(2次方程式の一般論を参照)、
として(2次方程式の一般論を参照)、
(i) 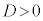 の場合は、②は、相異なる2実数解α,β(
の場合は、②は、相異なる2実数解α,β(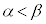 )を持ちます。
)を持ちます。 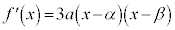 ・・・③
・・・③増減表は、以下のようになります。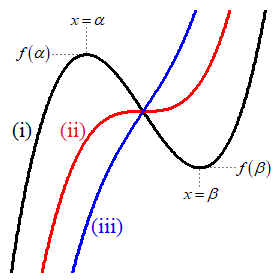 グラフは右図黒線(i)のようになります。
グラフは右図黒線(i)のようになります。
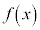 は、
は、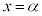 のとき極大値
のとき極大値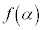 ,
,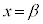 のとき極小値
のとき極小値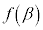 をとります。
をとります。 (ii) 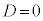 の場合は、②は、重解αを持ちます。
の場合は、②は、重解αを持ちます。 これより、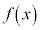 は単調増加で、グラフは右図赤線(ii)のようになります。
は単調増加で、グラフは右図赤線(ii)のようになります。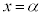 において、
において、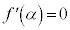 で
で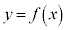 のグラフの接線の傾きは0になり、接線はx軸に平行になります。
のグラフの接線の傾きは0になり、接線はx軸に平行になります。 (iii) 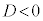 の場合は、②は、実数解を持ちません。
の場合は、②は、実数解を持ちません。 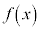 は単調増加で、
は単調増加で、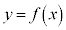 の接線の傾きは常に正で、グラフは右図青線(iii)のようになります。
の接線の傾きは常に正で、グラフは右図青線(iii)のようになります。
(i)の場合に、③を積分すると、
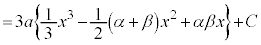 (C:積分定数)
(C:積分定数)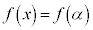 を考えると、
を考えると、
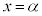 で極大になるので、当然
で極大になるので、当然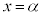 が重解になります。もう1つの解をγとすると、3次方程式の解と係数の関係より、
が重解になります。もう1つの解をγとすると、3次方程式の解と係数の関係より、
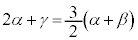 ∴
∴ 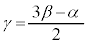
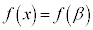 を考えると、
を考えると、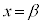 で極小になるので、
で極小になるので、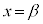 が重解になり、もう1つの解をδとすると、
が重解になり、もう1つの解をδとすると、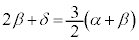 ∴
∴ 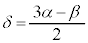
また③を微分して、
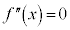 とすると、
とすると、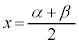 ,これは、2次関数
,これは、2次関数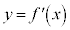 の軸の位置ですが、曲線
の軸の位置ですが、曲線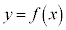 は、変曲点
は、変曲点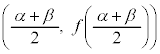 を持ちます。
を持ちます。
2次関数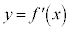 のグラフは軸
のグラフは軸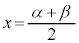 に関して線対称ですが、このために、3次関数
に関して線対称ですが、このために、3次関数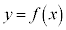 のグラフは変曲点に関して対称になります。つまり、
のグラフは変曲点に関して対称になります。つまり、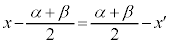 のとき、
のとき、
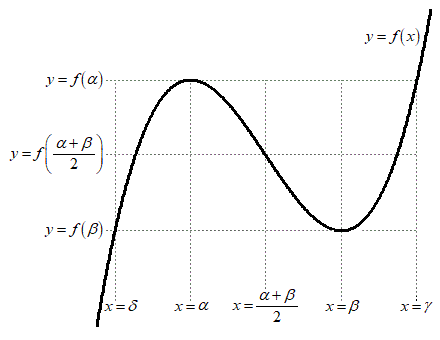 また、極小値
また、極小値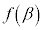 と同じ関数値となる位置
と同じ関数値となる位置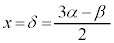 (
(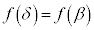 ),極大値の位置
),極大値の位置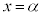 ,変曲点位置
,変曲点位置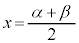 ,極小値の位置
,極小値の位置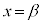 ,極大値と同じ関数値となる位置
,極大値と同じ関数値となる位置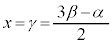 について、それぞれの差を調べると、
について、それぞれの差を調べると、
となり、すべて等しく、δ,α,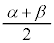 ,β,γは等間隔に並んでいることがわかります。これらを図示すると、右図のようになっています。
,β,γは等間隔に並んでいることがわかります。これらを図示すると、右図のようになっています。
また、④を用いると、極大値と極小値の和を求めよ、というときには、極大値の位置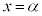 と極小値の位置
と極小値の位置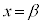 は、変曲点の位置に関して対称なところにあるので、極大値と極小値の和
は、変曲点の位置に関して対称なところにあるので、極大値と極小値の和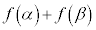 を、変曲点における関数値の2倍
を、変曲点における関数値の2倍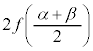 として求めることができます。
として求めることができます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 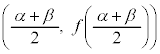 を持ちます。
を持ちます。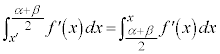 より、
より、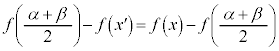
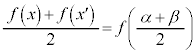 ・・・④
・・・④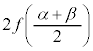 として求めることができます。
として求めることができます。